早教吧作业答案频道 -->数学-->
如图,四边形ABCD是O的内接四边形,延长DC,AB交于点E,且BE=BC.(1)求证:△ADE是等腰三角形;(2)若∠D=90°,O的半径为5,BC:DC=1:2,求△CBE的周长.
题目详情
如图,四边形ABCD是 O的内接四边形,延长DC,AB交于点E,且BE=BC.
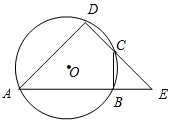
(1)求证:△ADE是等腰三角形;
(2)若∠D=90°, O的半径为5,BC:DC=1:
,求△CBE的周长.

(1)求证:△ADE是等腰三角形;
(2)若∠D=90°, O的半径为5,BC:DC=1:
| 2 |
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是 O的内接四边形,
∴∠A=∠BCE,
∵BE=BC,
∴∠BCE=∠BEC,
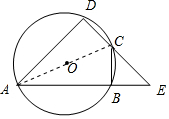 ∴∠A=∠BEC,
∴∠A=∠BEC,
∴DA=DE,即△ADE是等腰三角形;
(2)连接AC,
设BC=k,则CD=
k,
∵∠D=90°,
∴∠CBE=∠D=90°,又BE=BC,
∴∠E=45°,
∴BE=BC=k,EC=
k,
∴DE=2
k,
由勾股定理得,AC=
k,
∵ O的半径为5,
∴
k=10,
解得,k=
,
∴△CBE的周长为:2
+2
.
∴∠A=∠BCE,
∵BE=BC,
∴∠BCE=∠BEC,
 ∴∠A=∠BEC,
∴∠A=∠BEC,∴DA=DE,即△ADE是等腰三角形;
(2)连接AC,
设BC=k,则CD=
| 2 |
∵∠D=90°,
∴∠CBE=∠D=90°,又BE=BC,
∴∠E=45°,
∴BE=BC=k,EC=
| 2 |
∴DE=2
| 2 |
由勾股定理得,AC=
| 10 |
∵ O的半径为5,
∴
| 10 |
解得,k=
| 10 |
∴△CBE的周长为:2
| 10 |
| 5 |
看了 如图,四边形ABCD是O的内...的网友还看了以下:
关于圆的证明题如图,C为圆O的直径AB上一点,圆B过点C,与AB的延长线交于点D,与圆O的一个交点 2020-05-16 …
电动机物理题电流通过某一电路,电能(E)转化为机械能(E机)和内能(E内),已知这个电路两端的电压 2020-05-16 …
突触传递有何特征()A.单向传递B.总和C.相对不易疲劳D.中枢延搁E.对内环境变化敏感 2020-06-07 …
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外) 2020-06-09 …
如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于点EAE B D C 2020-06-27 …
在圆内接四边形ABCD中,延长AB,DC交与点E,延长AD,BC交与点F,若∠E=20,∠F=40 2020-08-03 …
ABCD是圆的内接四边形,AC是圆的直径,BD垂直于AC,BD与AC的交点为E,F在DA的延长线上 2020-08-03 …
(2011•武汉)如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B, 2020-11-03 …
高中函数题设函数f(x)=1/3x-lnx(x>0),则y=f(x)A.在区间(1/e,1),(1, 2020-12-26 …
在平面直角坐标系中,已知A(-1.0)B(0.2)点C在第二象限,CD⊥x轴,垂足为D,且△CDA≌ 2021-01-22 …