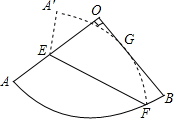
如图，已知扇形AOB的半径为6，圆心角为90°，E是半径OA上一点，F是AB上一点．将扇形AOB沿EF对折，使得折叠后的圆弧A′F恰好

Question

如图，已知扇形AOB的半径为6，圆心角为90°，E是半径OA上一点，F是

AB

上一点．将扇形AOB沿EF对折，使得折叠后的圆弧

A′F

恰好与半径OB相切于点G，若OE=5，则O到折痕EF的距离为___．

Answer 1

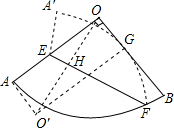过点G作O′G⊥OB，作AO′⊥O′G于O′，如图，连结OO′交EF于H，
则四边形AOGO′为矩形，
∴O′G=AO=6，
∵

AF

沿EF折叠后所得得圆弧

A′F

恰好与半径OB相切于点G，
∴

AF

与

A′F

所在圆的半径相等，
∴点O′为

A′F

所在圆的圆心，
∴点O与点O′关于EF对称，
∴OO′⊥EF，OH=HO′，
设OH=x，则OO′=2x，
∵∠EOH=∠O′OA，
∴Rt△OEH∽Rt△OO′A，
∴(OH)/(OA)=(OE)/(OO′)，即(x)/(6)=(5)/(2x)，解得x=√(15)，
即O到折痕EF的距离为√(15)．
故答案为√(15)．