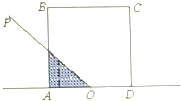
如图，正方形ABCD的边长为2，O为AD的中点，射线OP从OA出发，绕着点O顺时针方向旋转至OD，在旋转的过程中，记∠AOP为x（x∈[0，π]），OP所经过正方形ABCD内的区域（阴影部分）的面积S=f（x）

Question

如图，正方形ABCD的边长为2，O为AD的中点，射线OP从OA出发，绕着点O顺时针方向旋转至OD，在旋转的过程中，记∠AOP为x（x∈[0，π]），OP所经过正方形ABCD内的区域（阴影部分）的面积S=f（x），那么对于函数f（x）有以下三个结论：
①f（ (π)/(3)）= (√(3))/(2)；
②任意x∈[0， (π)/(2)]，都有f（ (π)/(2)-x）+f（ (π)/(2)+x）=4；
③任意x₁，x₂∈（ (π)/(2)，π），且x₁≠x₂，都有 (f(x1)-f(x2))/(x1-x2)<0．
其中所有正确结论的序号是___．

Answer 1

当0≤x≤arctan2时，f（x）=(1)/(2)×1×tanx=(1)/(2)tanx；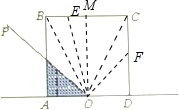
当arctan2<x<(π)/(2)，在△OBE中，f（x）=S_矩形OABM-S_△OME=2-(1)/(2)EM•OM=2-(2)/(tanx)；
当x=(π)/(2)时，f（x）=2；
当(π)/(2)<x≤π-arctan2时，同理可得f（x）=2-(2)/(tanx)．
当π-arctan2<x≤π时，f（x）=4-(1)/(2)×1×tan(π-x)=4+(1)/(2)tanx．于是可得：
①f((π)/(3))=(1)/(2)tan(π)/(3)=(√(3))/(2)，正确；
②由图形可得：∀x∈[0，π]），f（x）+f（π-x）=4，
因此对任意x∈[0，(π)/(2)]，都有f（(π)/(2)-x）+f（(π)/(2)+x）=4，故正确；
③不妨设x₁<x₂，则(f(x1)-f(x2))/(x1-x2)<0⇔f（x₁）>f（x₂），显然不正确．
综上只有：①②正确．
故答案为：①②．