早教吧作业答案频道 -->数学-->
已知f(x)=1+lnxx-1,g(x)=kx(k∈N*),对任意的c>1,存在实数a,b满足0<a<b<c,使得f(c)=f(a)=g(b),则k的最大值为.
题目详情
已知f(x)=
,g(x)=
(k∈N*),对任意的c>1,存在实数a,b满足0<a<b<c,使得f(c)=f(a)=g(b),则k的最大值为___.
| 1+lnx |
| x-1 |
| k |
| x |
▼优质解答
答案和解析
当k=1时,作函数f(x)=
,与g(x)=
(k∈N+)的图象如下,
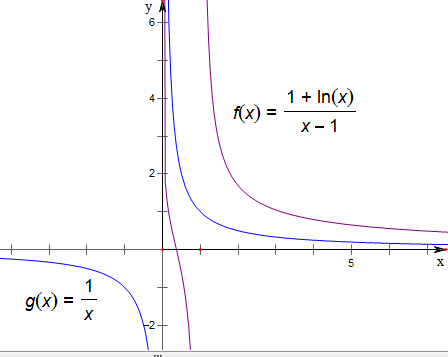
k=1,对∀c>1,存在实数a,b满足0<a<b<c,使得f(c)=f(a)=g(b)成立,正确;
当k=2时,作函数f(x)=
,与g(x)=
(k∈N+)的图象如下,

k=2,对∀c>1,存在实数a,b满足0<a<b<c,使得f(c)=f(a)=g(b)成立,正确;
当k=3时,作函数f(x)=
,与g(x)=
(k∈N+)的图象如下,
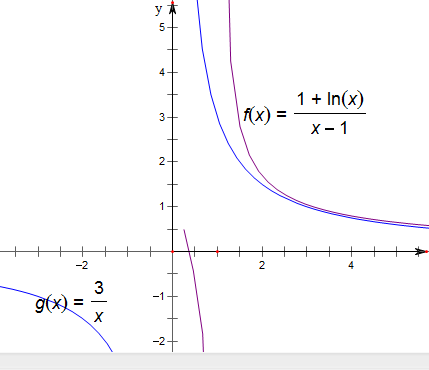
k=3时,对∀c>1,存在实数a,b满足0<a<b<c,使得f(c)=f(a)=g(b)成立,正确,
k=4时,作函数f(x)=
,与g(x)=
(k∈N+)的图象如下,
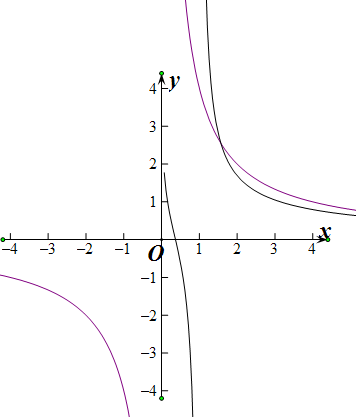
k=4,不正确,
故答案为:3.
| 1+lnx |
| x-1 |
| k |
| x |

k=1,对∀c>1,存在实数a,b满足0<a<b<c,使得f(c)=f(a)=g(b)成立,正确;
当k=2时,作函数f(x)=
| 1+lnx |
| x-1 |
| k |
| x |

k=2,对∀c>1,存在实数a,b满足0<a<b<c,使得f(c)=f(a)=g(b)成立,正确;
当k=3时,作函数f(x)=
| 1+lnx |
| x-1 |
| k |
| x |

k=3时,对∀c>1,存在实数a,b满足0<a<b<c,使得f(c)=f(a)=g(b)成立,正确,
k=4时,作函数f(x)=
| 1+lnx |
| x-1 |
| k |
| x |
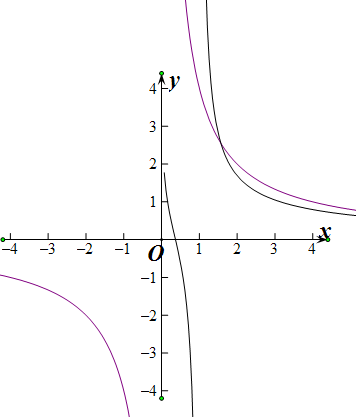
k=4,不正确,
故答案为:3.
看了 已知f(x)=1+lnxx-...的网友还看了以下:
f(x+1)=1/2f(x),则f(x)等于多少?下列函数式中,满足f(x+1)=1/2f(x)的是 2020-03-30 …
已知集合A=[x满足-2≤x≤5].B=[x满足a+1≤x≤2a–1].若A真包含于B,求a的范围 2020-04-27 …
已知矩阵A,B,X满足A-1XA=A-1-A*XB,其中A=101001110,B=1000200 2020-06-12 …
设矩阵A=11−1−1111−11,矩阵X满足A*X=A-1+2X,其中A*是A的伴随矩阵,求矩阵 2020-07-11 …
若对于任意的x∈[a,b],函数f(x),g(x)总满足,则称在区间[a,b]上,g(x)可以代替 2020-07-12 …
下列函数式中,满足f(x+1)=1/2f(x)的是?选D下列函数式中,满足f(x+1)=1/2f( 2020-07-20 …
设函数f(x)满足a*f(x)+b*f(1/x)=c/x(a.b.c均为常数),且(|a|≠|b| 2020-07-24 …
有限集合P中元素的个数记作card(P).已知card(M)=10,A⊆M,B⊆M,A∩B=∅,且 2020-08-01 …
解不等式如果不等式1/x1/3同时成立,那么x满足A.-1/3 2020-08-03 …
已知两个向量a=(X,2)b=(-2,3)求a与b满足下列条件时X的值①a∥b②a⊥b 2020-11-02 …