早教吧作业答案频道 -->数学-->
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.(1)求证:四边形ODEC是矩形;(2)当∠ADB=60°,AD=23时,求sin∠AED的值,求∠EAD的正切值.
题目详情
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
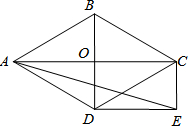
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2
时,求sin∠AED的值,求∠EAD的正切值.

(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2
| 3 |
▼优质解答
答案和解析
(1)证明:∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形.
又∵菱形ABCD,
∴AC⊥BD,
∴∠DOC=90°.
∴四边形ODEC是矩形.
(2)如图,过点E作EF⊥AD,交AD的延长线于F.
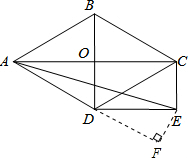 ∵AC⊥BD,∠ADB=60°,AD=2
∵AC⊥BD,∠ADB=60°,AD=2
,
∴OD=
,AO=OC=3.
∵四边形ODEC是矩形,
∴DE=OC=3,∠ODE=90°.
又∵∠ADO+∠ODE+∠EDF=180°,
∴∠EDF=30°.
在Rt△DEF中,∠F=90°,∠EDF=30°,
∴EF=
DE=
.
∴DF=
.
在Rt△AFE中,∠DFE=90°,
∴tan∠EAD=
=
=
=
.
∴四边形ODEC是平行四边形.
又∵菱形ABCD,
∴AC⊥BD,
∴∠DOC=90°.
∴四边形ODEC是矩形.
(2)如图,过点E作EF⊥AD,交AD的延长线于F.
 ∵AC⊥BD,∠ADB=60°,AD=2
∵AC⊥BD,∠ADB=60°,AD=2| 3 |
∴OD=
| 3 |
∵四边形ODEC是矩形,
∴DE=OC=3,∠ODE=90°.
又∵∠ADO+∠ODE+∠EDF=180°,
∴∠EDF=30°.
在Rt△DEF中,∠F=90°,∠EDF=30°,
∴EF=
| 1 |
| 2 |
| 3 |
| 2 |
∴DF=
3
| ||
| 2 |
在Rt△AFE中,∠DFE=90°,
∴tan∠EAD=
| EF |
| AF |
| EF |
| AD+DF |
| ||||||
2
|
| ||
| 7 |
看了 如图,菱形ABCD的对角线A...的网友还看了以下:
给出下面式子:①0真包含于{0}②R属于{R}③空集属于{空集}④空集真包含于{空集}⑤{0}含于 2020-06-22 …
有一可进行电池反应的两个半反应,电极和电解质溶液的物质均相同,但溶液的浓度不同,其电池的电动势() 2020-07-01 …
为什么0除以0没有答案?1乘1等于1,1除以1等于1.0乘0等于0,0除以0等于? 2020-07-26 …
高一数学题目,高分下面的5个写法中正确的两个是:①{0}属于{0.1.2};②空集真包含于{0}; 2020-07-30 …
ab是实数,且0小于a小于等于1,0小于b小于等于1,求证:根号下(a^2+b^2)+根号下(a- 2020-08-01 …
求个公式,知道的告诉下,如果A>0,则Z等于A*0.45如果B>0,则Z等于B*0.15如果C>0, 2020-11-01 …
你好请教两个考研数学问题~设b大于a大于e证明存在一个t属于(a,b),使得be^a-ae^b=(1 2020-11-26 …
用图像表示某二次函数(a大于0b大于0c大于0)图像交x轴于(-3,0)(-0.5,0)交y轴于(0 2020-12-08 …
若f(x)是R上的的偶函数且在0,+正无穷极)上是增函数,则下列成立的a.f(-2)大于f(0)大于 2020-12-08 …
IF公式大于小于的问题A,B,C,D四列,要写一个D列的IF公式,条件:如果C列小于等于±0.03, 2021-01-14 …