早教吧作业答案频道 -->数学-->
我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.(1)任意写出你所学过的特殊四边形中是“等邻角四边形”的一种图形的名称;(2)在探究“等邻角四边形”性质时:①
题目详情
我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.
(1)任意写出你所学过的特殊四边形中是“等邻角四边形”的一种图形的名称;
(2)在探究“等邻角四边形”性质时:
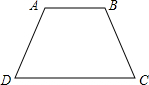
①小明画了一个“等邻角四边形”ABCD(如图1),其中∠A=∠B,AD=BC,此时他发现AB∥DC,请你证明此结论;
②由此小明猜想:“对于任意等邻角四边形,当一组对边相等时,另一组对边就平行”,请你直接判断这个命题是真命题还是假命题;
(3)已知:在“等邻角四边形”ABCD中,∠A=90°,∠C=60°,AB=6,BC=10,请画出相应图形,并直接写出CD的长.

(1)任意写出你所学过的特殊四边形中是“等邻角四边形”的一种图形的名称;
(2)在探究“等邻角四边形”性质时:
①小明画了一个“等邻角四边形”ABCD(如图1),其中∠A=∠B,AD=BC,此时他发现AB∥DC,请你证明此结论;
②由此小明猜想:“对于任意等邻角四边形,当一组对边相等时,另一组对边就平行”,请你直接判断这个命题是真命题还是假命题;
(3)已知:在“等邻角四边形”ABCD中,∠A=90°,∠C=60°,AB=6,BC=10,请画出相应图形,并直接写出CD的长.
▼优质解答
答案和解析
解(1)矩形,
∵矩形的四个角都是直角,
根据“等邻角四边形”的定义,
得到矩形是“等邻角四边形”;
(2)①如图,
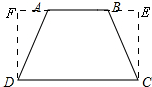
过点C作CE⊥AB,DF⊥AB,
∵∠DAB=∠CBA,
∴∠DAF=∠CBE,
∵CE⊥AB,DF⊥AB,
∴∠DFA=∠CEB=90°,
∵AD=BC,
∴△DFA≌△CEB,
∴DF=CE,
∵∠DFA=∠CEB=90°,
∴DF=EC,
∴四边形DFEC是平行四边形,
∴AB∥CD;
②假命题,
反例如图,
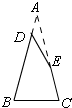
在等腰三角形的腰上取点D,E,使得DE=BC,四边形DBCE是等邻边四边形,没有对边平行.
(3)①∠D=∠A=90°,
如图,
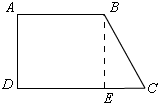
作BE⊥DC,
∵∠D=∠A=∠BED=90°,
∴四边形ADEB是矩形,
∴DE=AB=6.
在Rt△BEC中,BC=10,∠C=60°,
∴CE=5,
∴CD=DE+CE=11,
②如图,∠A=∠B=90°
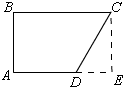
作CE⊥AD,
∵∠A=∠B=∠AEC=90°,
∴四边形ABCE是矩形,
∴AE=BC=10,CE=AB=6,
在Rt△CED中,∠DCE=∠BCE-∠BCD=30°,
∴CD=4
,
③∠B=∠C=60°.
如图,延长AD,BC交于E
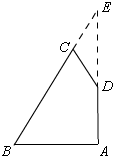
在Rt△ABE中,∠B=60°,AB=6,
∴BE=2AB=12,∠E=30°
∴CE=BE-BC=12-10=2,
∵∠BCD=60°,
∴∠CDE=∠CED=30°,
∴CD=CE=2,
④∠D=∠C=60°,
如图,延长DA,CB交于E,
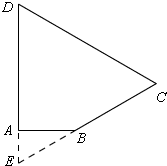
∵∠D=∠C=60°,
∴∠E=60°,CD=CE,
在Rt△ABE中,∠E=60°,AB=6,
∴BE=4
,
∴CD=BC+BE=10+4
.
∵矩形的四个角都是直角,
根据“等邻角四边形”的定义,
得到矩形是“等邻角四边形”;
(2)①如图,

过点C作CE⊥AB,DF⊥AB,
∵∠DAB=∠CBA,
∴∠DAF=∠CBE,
∵CE⊥AB,DF⊥AB,
∴∠DFA=∠CEB=90°,
∵AD=BC,
∴△DFA≌△CEB,
∴DF=CE,
∵∠DFA=∠CEB=90°,
∴DF=EC,
∴四边形DFEC是平行四边形,
∴AB∥CD;
②假命题,
反例如图,

在等腰三角形的腰上取点D,E,使得DE=BC,四边形DBCE是等邻边四边形,没有对边平行.
(3)①∠D=∠A=90°,
如图,

作BE⊥DC,
∵∠D=∠A=∠BED=90°,
∴四边形ADEB是矩形,
∴DE=AB=6.
在Rt△BEC中,BC=10,∠C=60°,
∴CE=5,
∴CD=DE+CE=11,
②如图,∠A=∠B=90°

作CE⊥AD,
∵∠A=∠B=∠AEC=90°,
∴四边形ABCE是矩形,
∴AE=BC=10,CE=AB=6,
在Rt△CED中,∠DCE=∠BCE-∠BCD=30°,
∴CD=4
| 3 |
③∠B=∠C=60°.
如图,延长AD,BC交于E

在Rt△ABE中,∠B=60°,AB=6,
∴BE=2AB=12,∠E=30°
∴CE=BE-BC=12-10=2,
∵∠BCD=60°,
∴∠CDE=∠CED=30°,
∴CD=CE=2,
④∠D=∠C=60°,
如图,延长DA,CB交于E,

∵∠D=∠C=60°,
∴∠E=60°,CD=CE,
在Rt△ABE中,∠E=60°,AB=6,
∴BE=4
| 3 |
∴CD=BC+BE=10+4
| 3 |
看了 我们把:“有一组邻角相等的凸...的网友还看了以下:
1.任意四边形中任意点到四个顶点分成4个三角形一组无公共边的两个三角形与另一组的面积关系;2.平行 2020-05-13 …
关于任意四边形分为两等面积部分的问题请问在任意一个四边形中,已经给定一条过顶点的好线(好线:在任意 2020-06-13 …
组织:A结构特点:细胞间隙较大,细胞间质多功能:运输,支持,连接,营养等组织:B结构特点:排列整齐 2020-06-18 …
那位大侠数学好的麻烦给算算急40个球2个球上写欧3个球上写驰7个球上写沙7个球上写发抽四个球一等奖 2020-06-18 …
懂数学两个字的进如果给出三个阿拉伯数字,请问可以组成几个任意的三位数?如果四个可以组成几个任意四位 2020-06-18 …
0-9用这十个数其中的任意四个数相加等于20,总共有几组?具体的有哪些?注意:不能重复!急用~ 2020-06-27 …
修改病句加解释:小碑座的四周,雕刻着以牡丹花、荷花、菊花、等组成的八大大花圈,这些花象征着品质高.. 2020-11-10 …
已知任意四边形ABCD,E、F是AD的三等分点,G、H是BC的三等分点.求证:S四边形EFGH=1/ 2020-12-14 …
将状况相同的某种绿叶分成四等组,在不同温度下分别先暗处理1h,再光照1h(各组光强照度相同),测其重 2020-12-20 …
将状况相同的某种绿叶分成四等组,在不同温度下分别先暗处理1h,再光照1h(各组光强照度相同),测其重 2020-12-20 …