在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y=kx（k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH=43，点B的坐标为（

Question

在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y=(k)/(x)（k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH=(4)/(3)，点B的坐标为（m，-2）．

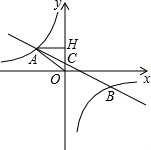
（1）求△AHO的周长；
（2）求该反比例函数和一次函数的解析式．

Answer 1

（1）由OH=3，tan∠AOH=(4)/(3)，得
AH=4．即A（-4，3）．
由勾股定理，得
AO=√(OH2+AH2)=5，
△AHO的周长=AO+AH+OH=3+4+5=12；
（2）将A点坐标代入y=(k)/(x)（k≠0），得
k=-4×3=-12，
反比例函数的解析式为y=(-12)/(x)；
当y=-2时，-2=(-12)/(x)，解得x=6，即B（6，-2）．
将A、B点坐标代入y=ax+b，得

-4a+b=3

6a+b=-2

，
解得

a=-(1)/(2)

b=1

，
一次函数的解析式为y=-(1)/(2)x+1．