早教吧作业答案频道 -->数学-->
已知正方形ABCD和正方形CGEF,且D点在CF边上,M为AE中点,连接MD、MF(1)如图1,请直接给出线段MD、MF的数量及位置关系是;(2)如图2,把正方形CGEF绕点C顺时针旋转,则(1)中的结论是
题目详情
已知正方形ABCD和正方形CGEF,且D点在CF边上,M为AE中点,连接MD、MF
(1)如图1,请直接给出线段MD、MF的数量及位置关系是___;
(2)如图2,把正方形CGEF绕点C顺时针旋转,则(1)中的结论是否成立?若成立,请证明;若不成立,请给出你的结论并证明;
(3)若将正方形CGEF绕点C顺时针旋转30°时,CF边恰好平分线段AE,请直接写出
的值.
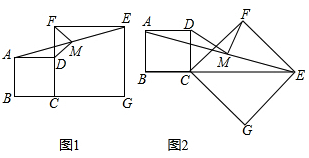
(1)如图1,请直接给出线段MD、MF的数量及位置关系是___;
(2)如图2,把正方形CGEF绕点C顺时针旋转,则(1)中的结论是否成立?若成立,请证明;若不成立,请给出你的结论并证明;
(3)若将正方形CGEF绕点C顺时针旋转30°时,CF边恰好平分线段AE,请直接写出
| CG |
| CB |

▼优质解答
答案和解析
(1)线段MD、MF的数量及位置关系是MD=MF,MD⊥MF,
理由:如图1,延长DM交EF于点P,
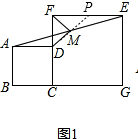
∵四边形ABCD和四边形FCGE是正方形,
∴AD∥EF,∠MAD=∠MEP.∠CFE=90°.
∴△DFP是直角三角形.
∵M为AE的中点,
∴AM=EM.
在△ADM和△EPM中,
,
∴△ADM≌△EPM(ASA),
∴DM=PM,AD=PE,
∴M是DP的中点.
∴MF=
DP=MD,
∵AD=CD,
∴CD=PE,
∵FC=FE,
∴FD=FP,
∴△DFP是等腰直角三角形,
∴FM⊥DP,即FM⊥DM.
故答案为:MD=MF,MD⊥MF;
(2)MD=MF,MD⊥MF仍成立.
证明:如图2,延长DM交CE于点N,连接FN、DF,
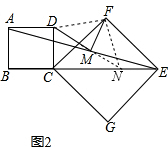
∵CE是正方形CFEG对角线,
∴∠FCN=∠CEF=45°,
∵∠DCE=90°,
∴∠DCF=45°,
∵AD∥BC,
∴∠DAM=∠NEM,
在△ADM和△ENM中,
,
∴△ADM≌△ENM(ASA),
∴EN=AD,DM=MN,
∵AD=CD,
∴CD=EN,
在△CDF和△ENF中,
,
∴△CDF≌△ENF,(SAS)
∴DF=NF,
∴FM=DM,FM⊥DM.
(3)如图所示,若CF边恰好平分线段AE,则CF过点M,
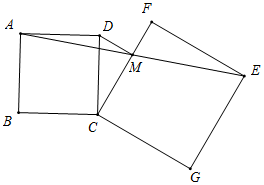
由(1)可得FM=DM,FM⊥DM,
设FM=DM=1,
∵∠DCF=30°,
∴Rt△DCM中,CM=
,CD=2=CB,
∴CF=
+1=CG,
∴
=
.
理由:如图1,延长DM交EF于点P,

∵四边形ABCD和四边形FCGE是正方形,
∴AD∥EF,∠MAD=∠MEP.∠CFE=90°.
∴△DFP是直角三角形.
∵M为AE的中点,
∴AM=EM.
在△ADM和△EPM中,
|
∴△ADM≌△EPM(ASA),
∴DM=PM,AD=PE,
∴M是DP的中点.
∴MF=
| 1 |
| 2 |
∵AD=CD,
∴CD=PE,
∵FC=FE,
∴FD=FP,
∴△DFP是等腰直角三角形,
∴FM⊥DP,即FM⊥DM.
故答案为:MD=MF,MD⊥MF;
(2)MD=MF,MD⊥MF仍成立.
证明:如图2,延长DM交CE于点N,连接FN、DF,

∵CE是正方形CFEG对角线,
∴∠FCN=∠CEF=45°,
∵∠DCE=90°,
∴∠DCF=45°,
∵AD∥BC,
∴∠DAM=∠NEM,
在△ADM和△ENM中,
|
∴△ADM≌△ENM(ASA),
∴EN=AD,DM=MN,
∵AD=CD,
∴CD=EN,
在△CDF和△ENF中,
|
∴△CDF≌△ENF,(SAS)
∴DF=NF,
∴FM=DM,FM⊥DM.
(3)如图所示,若CF边恰好平分线段AE,则CF过点M,

由(1)可得FM=DM,FM⊥DM,
设FM=DM=1,
∵∠DCF=30°,
∴Rt△DCM中,CM=
| 3 |
∴CF=
| 3 |
∴
| CG |
| CB |
| ||
| 2 |
看了 已知正方形ABCD和正方形C...的网友还看了以下:
A、B两种短周期元素,可以形成两种不同的共价化合物C和D.A在化合物C中显-1价,在化合物D中显- 2020-04-08 …
已知直线L:y=-1/2x+m与曲线c:y=1+(1/2)*(√|4-x²|)仅有三个交点,则实数 2020-05-15 …
关于多元函数极值的问题:在椭球面x平方/a平方+y平方/b平方+z平方/c平方=1(a>0,b>0 2020-05-16 …
在等式y=axx+bx+c中,x=1,y=-2.x=-1,y=20.x=3/2和x=1/3,y的值 2020-05-16 …
在三角形ABC中,a b c分别是角A B C所对边地长,已知三角形ABC的面积S=a平方-(b- 2020-05-16 …
由a=b一定可以得出的等式是()A.a÷c=b÷c由a=b一定可以得出的等式是()A.a÷c=b÷ 2020-06-06 …
设数列{an}满足a1=A,an+1=Ban+C(n属于自然数A,B,C为常数),试求该数列的通项 2020-06-18 …
在△ABC中,三边abc与面积S的关系式为S=(根号3)/4(a平方+b平方-c平方)1:求∠C的 2020-07-20 …
在一元二次方程y=ax平方+bx+c中,方程的两个根,x1,x2.他们之间和是多少.积又是多少. 2020-11-07 …
三个不等于零数的平方等于一a平方+b平方+c平方=1(abc不等于零)A(B/1+C/1)+B(C/ 2020-11-18 …