早教吧作业答案频道 -->数学-->
已知点O是四边形ABCD内一点,AB=BC,OD=OC,∠ABC=∠DOC=α.(1)如图1,α=60°,探究线段AD与OB的数量关系,并加以证明;(2)如图2,α=120°,探究线段AD与OB的数量关系,并说明理由;(3
题目详情
已知点O是四边形ABCD内一点,AB=BC,OD=OC,∠ABC=∠DOC=α.
(1)如图1,α=60°,探究线段AD与OB的数量关系,并加以证明;
(2)如图2,α=120°,探究线段AD与OB的数量关系,并说明理由;
(3)结合上面的活动经验探究,请直接写出如图3中线段AD与OB的数量关系为___(直接写出答案)
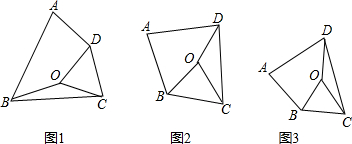
(1)如图1,α=60°,探究线段AD与OB的数量关系,并加以证明;
(2)如图2,α=120°,探究线段AD与OB的数量关系,并说明理由;
(3)结合上面的活动经验探究,请直接写出如图3中线段AD与OB的数量关系为___(直接写出答案)

▼优质解答
答案和解析
 (1)AD=OB,
(1)AD=OB,
如图1,连接AC,
∵AB=BC,OD=OC,∠ABC=∠DOC=60°,
∴△ABC与△COD是等边三角形,
∴∠ACB=∠DCO=60°,
∴∠ACD=∠BCO,
在△ACD与△BCO中,
,
∴△ACD≌△BCO,
∴AD=OB;
(2)AD=
OB;
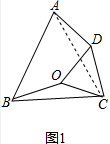
如图2,连接AC,过B作BF⊥AC于F,
 ∵AB=BC,OD=OC,∠ABC=∠DOC=120°,
∵AB=BC,OD=OC,∠ABC=∠DOC=120°,
∴∠ACB=∠DCO=30°,
∴∠ACD=∠BCO,
∴△ACD∽△BCO,
∴
=
,
∵∠CFB=90°,
∴
=2sin60°=
,
∴AD=
OB;
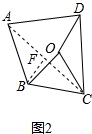
(3) 如图3,连接AC,过B作BF⊥AC于F,
如图3,连接AC,过B作BF⊥AC于F,
∵AB=BC,OD=OC,∠ABC=∠DOC=α,
∴∠ACB=∠DCO=
,
∴∠ACD=∠BCO,
∴△ACD∽△BCO,
∴
=
,
∵∠CFB=90°,
∴
=2sin
,
∴AD=2sin
OB.
故答案为:AD=2sin
OB.
 (1)AD=OB,
(1)AD=OB,如图1,连接AC,
∵AB=BC,OD=OC,∠ABC=∠DOC=60°,
∴△ABC与△COD是等边三角形,
∴∠ACB=∠DCO=60°,
∴∠ACD=∠BCO,
在△ACD与△BCO中,
|
∴△ACD≌△BCO,
∴AD=OB;
(2)AD=
| 3 |
如图2,连接AC,过B作BF⊥AC于F,
 ∵AB=BC,OD=OC,∠ABC=∠DOC=120°,
∵AB=BC,OD=OC,∠ABC=∠DOC=120°,∴∠ACB=∠DCO=30°,
∴∠ACD=∠BCO,
∴△ACD∽△BCO,
∴
| AD |
| OB |
| AC |
| BC |
∵∠CFB=90°,
∴
| 2CF |
| BC |
| 3 |
∴AD=
| 3 |
(3)
 如图3,连接AC,过B作BF⊥AC于F,
如图3,连接AC,过B作BF⊥AC于F,∵AB=BC,OD=OC,∠ABC=∠DOC=α,
∴∠ACB=∠DCO=
| 180°-α |
| 2 |
∴∠ACD=∠BCO,
∴△ACD∽△BCO,
∴
| AD |
| OB |
| AC |
| BC |
∵∠CFB=90°,
∴
| 2CF |
| BC |
| α |
| 2 |
∴AD=2sin
| α |
| 2 |
故答案为:AD=2sin
| α |
| 2 |
看了 已知点O是四边形ABCD内一...的网友还看了以下:
直线MN上有P'、O、P、Q四点,质点A、B在某时刻分别位于P点和Q点,并具有相同的速直线MN上有 2020-07-09 …
如图,已知AB是⊙O的弦,点C是弦AB上任意一点(不与点A.B重合),连接CO并延长CO交⊙O于点 2020-07-11 …
如图,已知△ABC,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC,BC分别相切于点D与 2020-07-22 …
已知A为圆O上的一点,圆O的半径为1,该平面上另有一点P,PA=根号3,那么点P与圆O有怎样的关系 2020-07-26 …
如图,在三角形ABC中,点o是边AC上一个动点,过o作直线EF//BC,设EF交角BCA的平分线于 2020-07-30 …
如图所示,O点离地面高度为H,以O点为圆心,制作一个半径为R的四分之一光滑圆弧轨道,小球从与O点等 2020-07-31 …
如图,已知△ABC,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC,BC分别相切于点D与 2020-07-31 …
如图,在△ABC中,点O是AC边上的一个动点,过O点作直线MN‖BC,设MN交∠BCA的平分线于点 2020-08-03 …
如图,A点在O点的西偏北40度方向上,请你在下图画出OB线,使OB与OA互相垂直,并说出B点在O点的 2021-01-02 …
根据要求画图,并回答问题.已知:直线AB、CD相交于点O,且OE⊥AB(1)过点O画直线MN⊥CD; 2021-01-15 …