早教吧作业答案频道 -->数学-->
如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D.(1)当点M在AB上运动时,则四边形OCMD的周长=.(2)当四边形O
题目详情
如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D.
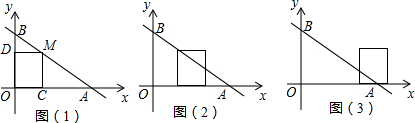
(1)当点M在AB上运动时,则四边形OCMD的周长=___.
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a(0<a≤4),在平移过程中,当平移距离a为多少时,正方形OCMD的面积被直线AB分成1:3两个部分?

(1)当点M在AB上运动时,则四边形OCMD的周长=___.
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a(0<a≤4),在平移过程中,当平移距离a为多少时,正方形OCMD的面积被直线AB分成1:3两个部分?
▼优质解答
答案和解析
(1)设OC=x,则CM=4-x.
∵MC⊥OA,MD⊥OB,OD⊥OC,
∴四边形OCMD为矩形,
∴四边形OCMD的周长=OD+OC+CM+DM=2(CO+CM)=2(x+4-x)=2×4=8.
故答案为:8.
(2)∵当四边形为OCMD为正方形时,OC=CM,即x=4-x,解得:x=2,
∴S正方形OCMD的面积=4.
∵正方形OCMD的面积被直线AB分成1:3两个部分,
∴两部分的面积分别为1和3.
当0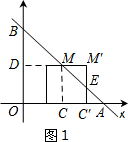
∵直线AB的解析式为y=4-x,
∴∠BAO=45°.
∴△MM′E为等腰直角三角形.
∴MM′=M′E.
∴
MM′2=1.
∴MM′=
,即a=
当2<a<4时,如图2所示:
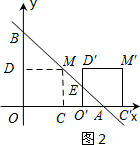
∵∠BAO=45°,
∴△EO′A为等腰直角三角形.
∴EO′=O′A.
∴
O′A2=1,解得:O′A=
.
∵将y=0代入y=4-x得;4-x=0,解得;x=4,
∴OA=4.
∴OO′=4-
,即a=4-
.
综上所述,当平移的距离为a=
或a=4-
时,正方形OCMD的面积被直线AB分成1:3两个部分.
∵MC⊥OA,MD⊥OB,OD⊥OC,
∴四边形OCMD为矩形,
∴四边形OCMD的周长=OD+OC+CM+DM=2(CO+CM)=2(x+4-x)=2×4=8.
故答案为:8.
(2)∵当四边形为OCMD为正方形时,OC=CM,即x=4-x,解得:x=2,
∴S正方形OCMD的面积=4.
∵正方形OCMD的面积被直线AB分成1:3两个部分,
∴两部分的面积分别为1和3.
当0

∵直线AB的解析式为y=4-x,
∴∠BAO=45°.
∴△MM′E为等腰直角三角形.
∴MM′=M′E.
∴
| 1 |
| 2 |
∴MM′=
| 2 |
| 2 |
当2<a<4时,如图2所示:

∵∠BAO=45°,
∴△EO′A为等腰直角三角形.
∴EO′=O′A.
∴
| 1 |
| 2 |
| 2 |
∵将y=0代入y=4-x得;4-x=0,解得;x=4,
∴OA=4.
∴OO′=4-
| 2 |
| 2 |
综上所述,当平移的距离为a=
| 2 |
| 2 |
看了 如图,直线y=4-x与两坐标...的网友还看了以下:
如图,四边形OABC是长方形,顶点坐标为A(6,0),B(6,4),C(0,4),O(0,0),线 2020-05-13 …
等差数列{an}的前n项和为Sn,若m>1,且a(m-1)+a(m+1)-a^2(m)=0.[注( 2020-05-13 …
在平面直角坐标系中,直线y=2x-3上有一动点A,以点A为圆心,3为半径作圆A.(1)当圆A与直线 2020-05-17 …
1.点M的横坐标是a,纵坐标是b,且a,b是方程x²-8=0的两个根,求M点的坐标.2.点M(x, 2020-06-14 …
在平面直角坐标系内有两点A、B,其坐标为A(-1,-1),B(2,4),点M为x轴上的一个动点,若 2020-07-20 …
求自然数m,使得a(m-1),(am)2,a(m+1)+3依次成等差数列这里的上标下标显示不出来第 2020-07-23 …
如图(1)(2),直线y=-x+4与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两 2020-08-01 …
在平面直角坐标系中,点M的坐标为(a,1-2a)当a=负1时,(1)点M在坐标系的第几象限,(2) 2020-08-02 …
某元素的一种同位素X的原子质量数为A,含N个中子,它与H(质量数为1,中子数为0)原子组成HMX(M 2020-12-16 …
椭圆M:x^2/a^2+y^2/b^2=1(a>b>0)的离心率是根号2/2且经过P(1,根号2/2 2021-01-13 …