如图，正方形ABCD的边长是3，BP=CQ，连接AQ，DP交于点O，并分别与边CD，BC交于点F，E，连接AE，下列结论：①AQ⊥DP；②OA2=OE•OP；③S△AOD=S四边形OECF；④当BP=1时，tan∠OAE=1316，其中正确结论的

Question

如图，正方形ABCD的边长是3，BP=CQ，连接AQ，DP交于点O，并分别与边CD，BC交于点F，E，连接AE，下列结论：①AQ⊥DP；②OA²=OE•OP；③S_△AOD=S_{四边形OECF}；④当BP=1时，tan∠OAE=

(13)/(16)，其中正确结论的个数是（　　）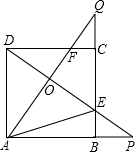

A. 1

B. 2

C. 3

D. 4

Answer 1

∵四边形ABCD是正方形，
∴AD=BC，∠DAB=∠ABC=90°，
∵BP=CQ，
∴AP=BQ，
在△DAP与△ABQ中，

AD=AB

∠DAP=∠ABQ

AP=BQ

，
∴△DAP≌△ABQ，
∴∠P=∠Q，
∵∠Q+∠QAB=90°，
∴∠P+∠QAB=90°，
∴∠AOP=90°，
∴AQ⊥DP；
故①正确；
∵∠DOA=∠AOP=90，∠ADO+∠P=∠ADO+∠DAO=90°，
∴∠DAO=∠P，
∴△DAO∽△APO，
∴(AO)/(OD)=(OP)/(OA)，
∴AO²=OD•OP，
∵AE>AB，
∴AE>AD，
∴OD≠OE，
∴OA²≠OE•OP；故②错误；
在△CQF与△BPE中

∠FCQ=∠EBP

∠Q=∠P

CQ=BP

，
∴△CQF≌△BPE，
∴CF=BE，
∴DF=CE，
在△ADF与△DCE中，

AD=CD

∠ADC=∠DCE

DF=CE

，
∴△ADF≌△DCE，
∴S_△ADF-S_△DFO=S_△DCE-S_△DOF，
即S_△AOD=S_{四边形OECF}；故③正确；
∵BP=1，AB=3，
∴AP=4，
∵△AOP∽△DAP，
∴(PB)/(EB)=(PA)/(DA)=(4)/(3)，
∴BE=(3)/(4)，∴QE=(13)/(4)，
∵△QOE∽△PAD，
∴(QO)/(PA)=(OE)/(AD)=(QE)/(PD)=((13)/(4))/(5)，
∴QO=(13)/(5)，OE=(39)/(20)，
∴AO=5-QO=(12)/(5)，
∴tan∠OAE=

作业帮用户 2017-10-05

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议

OE