早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.(1)如图1,若点F与点A重合,求证:AC=BC;(2)若∠DAF=∠DBA,①如图2,当点F在线
题目详情
在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
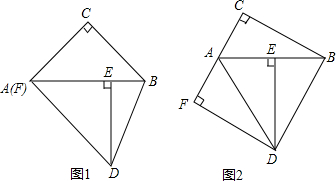
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.

▼优质解答
答案和解析
(1)由旋转得,∠BAC=∠BAD,
∵DF⊥AC,
∴∠CAD=90°,
∴∠BAC=∠BAD=45°,
∵∠ACB=90°,
∴∠ABC=45°,
∴AC=CB,
(2)①由旋转得,AD=AB,
∴∠ABD=∠ADB,
∵∠DAF=∠ABD,
∴∠DAF=∠ADB,
∴AF∥BD,
∴∠BAC=∠ABD,
∵∠ABD=∠FAD
由旋转得,∠BAC=∠BAD,
∴∠FAD=∠BAC=∠BAD=
×180°=60°,
由旋转得,AB=AD,
∴△ABD是等边三角形,
∴AD=BD,
在△AFD和△BED中,
,
∴△AFD≌△BED,
∴AF=BE,
②如图,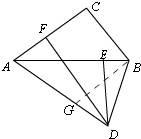
由旋转得,∠BAC=∠BAD,
∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD,
由旋转得,AD=AB,
∴∠ABD=∠ADB=2∠BAD,
∵∠BAD+∠ABD+∠ADB=180°,
∴∠BAD+2∠BAD+2∠BAD=180°,
∴∠BAD=36°,
设BD=y,作BG平分∠ABD,
∴∠BAD=∠GBD=36°
∴AG=BG=BD=y,
∴DG=AD-AG=AD-BG=AD-BD,
∵∠BDG=∠ADB,
∴△BDG∽△ADB,
∴
=
.
∴
=
=
-1,即(
)2-
-1=0,
∴
=
,
∵∠FAD=∠EBD,∠AFD=∠BED,
∴△AFD∽△BED,
∴
=
,
∴AF=
×BE=
x.
∵DF⊥AC,
∴∠CAD=90°,
∴∠BAC=∠BAD=45°,
∵∠ACB=90°,
∴∠ABC=45°,
∴AC=CB,
(2)①由旋转得,AD=AB,
∴∠ABD=∠ADB,
∵∠DAF=∠ABD,
∴∠DAF=∠ADB,
∴AF∥BD,
∴∠BAC=∠ABD,
∵∠ABD=∠FAD
由旋转得,∠BAC=∠BAD,
∴∠FAD=∠BAC=∠BAD=
| 1 |
| 3 |
由旋转得,AB=AD,
∴△ABD是等边三角形,
∴AD=BD,
在△AFD和△BED中,
|
∴△AFD≌△BED,
∴AF=BE,
②如图,

由旋转得,∠BAC=∠BAD,
∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD,
由旋转得,AD=AB,
∴∠ABD=∠ADB=2∠BAD,
∵∠BAD+∠ABD+∠ADB=180°,
∴∠BAD+2∠BAD+2∠BAD=180°,
∴∠BAD=36°,
设BD=y,作BG平分∠ABD,
∴∠BAD=∠GBD=36°
∴AG=BG=BD=y,
∴DG=AD-AG=AD-BG=AD-BD,
∵∠BDG=∠ADB,
∴△BDG∽△ADB,
∴
| BD |
| AD |
| DG |
| DB |
∴
| BD |
| AD |
| AD-BD |
| BD |
| AD |
| BD |
| AD |
| BD |
| AD |
| BD |
∴
| AD |
| BD |
1+
| ||
| 2 |
∵∠FAD=∠EBD,∠AFD=∠BED,
∴△AFD∽△BED,
∴
| AD |
| BD |
| AF |
| BE |
∴AF=
| AD |
| BD |
1+
| ||
| 2 |
看了 在Rt△ABC中,∠C=90...的网友还看了以下:
若a大于0在,则a分之a的绝对值等于 2020-04-05 …
已知函数f(x)=x^2-kx+4,若f(x)>0在[1,a]上恒成立,求k的范围 2020-05-22 …
小军用电脑设计了ABCD四种装置,将一个数输入一种装置后,会输入另一个数.装置A:将输入的数加上1 2020-06-16 …
设a<0,(3x2+a)(2x+b)≥0在(a,b)上恒成立,则b-a的最大值为()A.13B.1 2020-06-27 …
已知点A(10,0,0)和点B(10,0,10),以下关于点A和点B的相对位置正确的是().A、点 2020-07-09 …
设a<0,(3x2+a)(2x+b)≥0在(a,b)上恒成立,则b-a的最大值为. 2020-07-21 …
在x轴的x=a和x=-a两位置上,各有一个电量均为Q的固定点电荷,在x=0处有一电量为q、质量为m 2020-07-30 …
如下图所示,△ABO的三个顶点的坐标分别为O(0,0),A(5,0),B(2,4).(1)求△OAB 2020-11-03 …
已知勾函数……求实数t的取值范围.已知勾函数y=x+a∧2/x(a>0)在(-∞,-a)和(a,+∞ 2020-11-08 …
设函数f在[a,b]上连续且无零点,F(X)=∫xaf(t)dt+∫xb1f(t)dt,则方程F(x 2020-12-26 …