早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,AC=BC,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.(1)求证:△ACE∽△BFC;(2)试探究AF、BF、EF之间有何数量
题目详情
如图,在△ABC中,∠ACB=90°,AC=BC,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.
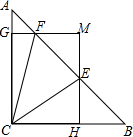
(1)求证:△ACE∽△BFC;
(2)试探究AF、BF、EF之间有何数量关系?说明理由.

(1)求证:△ACE∽△BFC;
(2)试探究AF、BF、EF之间有何数量关系?说明理由.
▼优质解答
答案和解析
(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵∠CFB=∠ACF+∠A=∠ACF+45°,
∠ACE=∠ACF+∠ECF=∠ACF+45°,
∴∠CFB=∠ACE,
∴△ACE∽△BFC;
(2) EF2=AF2+BE2,理由如下: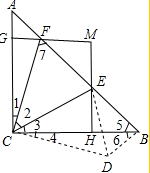
∵AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°,
将△ACF顺时针旋转90°至△BCD,如图所示:
则CF=CD,∠1=∠4,∠A=∠6=45°,BD=AF,
∵∠2=45°,
∴∠1+∠3=∠3+∠4=45°,
∴∠DCE=∠2,
在△ECF和△ECD中,
,
∴△ECF≌△ECD(SAS),
∴EF=DE,
∵∠5=45°,
∴∠EBD=90°,
∴DE2=BD2+BE2,
即EF2=AF2+BE2.
∴∠A=∠B=45°,
∵∠CFB=∠ACF+∠A=∠ACF+45°,
∠ACE=∠ACF+∠ECF=∠ACF+45°,
∴∠CFB=∠ACE,
∴△ACE∽△BFC;
(2) EF2=AF2+BE2,理由如下:

∵AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°,
将△ACF顺时针旋转90°至△BCD,如图所示:
则CF=CD,∠1=∠4,∠A=∠6=45°,BD=AF,
∵∠2=45°,
∴∠1+∠3=∠3+∠4=45°,
∴∠DCE=∠2,
在△ECF和△ECD中,
|
∴△ECF≌△ECD(SAS),
∴EF=DE,
∵∠5=45°,
∴∠EBD=90°,
∴DE2=BD2+BE2,
即EF2=AF2+BE2.
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
提先谢谢了,越快越好1.求下列函数的值:(1)已知f(x)=|x-2|分之x+1,求f(0),f( 2020-04-27 …
已知函数f(x)=2acosx+bsinxcosx,f(0)=2,f(派/3)=1/2+根号3/2 2020-05-15 …
1.已知f(x)=4msinx-cos2x(1)若m=0,求f(x)的单调递增区间(2)若f(x) 2020-05-20 …
一个关于求导数的答案不明白的地方求f(x)=2x^2+x-1(x>0)的反函数在x=2处的切线的斜 2020-06-06 …
设常数a∈R,函数f(x)=(a-x)|x|.(Ⅰ)若a=1,求f(x)的单调区间;(Ⅱ)若f(x 2020-06-12 …
已知二次函数F(x)=ax^2+bx,若函数f(x)的最小值为f(-1)=-1,F(x)=f(x) 2020-07-13 …
函数f(X)对任意a,b都有f(a+b)=f(a)+f(b)-1,且当X〉0时有f(x)〉1.求证 2020-08-01 …
高考已知函数f(x)=a(x-1)/x^2,其中a>0求函数f(x)的单调区间.若直线x-y-1= 2020-08-02 …
已知fx是定义在实数集R上的奇函数,且当x大于0时fx=x^2-4x+31,求f[f(-已知fx是定 2020-11-07 …
问两道分段函数基础题,数学底子差啊……(20)在线1,已知f(x)=大括号x^2,X>0,e,X=0 2020-12-08 …