早教吧作业答案频道 -->数学-->
已知四边形ABCD,AD∥BC,∠D=90°,∠BAD=120°,AC平分∠BAD,AB=2AD.(1)如图1,求证:△ABC是等边三角形;(2)如图2,点E在BA的延长线上,在BC取一点F,连接EC,EF,且EC=EF,求证:BF=AE.(3
题目详情
已知四边形ABCD,AD∥BC,∠D=90°,∠BAD=120°,AC平分∠BAD,AB=2AD.
(1)如图1,求证:△ABC是等边三角形;
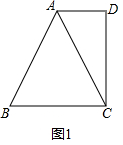
(2)如图2,点E在BA的延长线上,在BC取一点F,连接EC,EF,且EC=EF,求证:BF=AE.
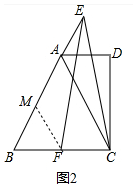
(3)连接AF,取CE的中点M,作MH⊥AF,探究MH⊥AF,探究:FH、AH之间的数量关系,并证明你的结论.
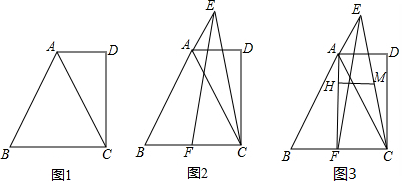
(1)如图1,求证:△ABC是等边三角形;
(2)如图2,点E在BA的延长线上,在BC取一点F,连接EC,EF,且EC=EF,求证:BF=AE.
(3)连接AF,取CE的中点M,作MH⊥AF,探究MH⊥AF,探究:FH、AH之间的数量关系,并证明你的结论.

▼优质解答
答案和解析
(1)证明:如图1中,
∵∠BAD=120°,AC平分∠BAD,
∴∠CAB=∠CAD=60°,
∵AD∥BC,
∴∠DAC=∠BCA=60°,
∴∠B=∠BCA=∠BAC=60°,
∴△ABC是等边三角形.
(2)证明:如图2中,作FM∥AC交AB于M.
∵MF∥AC,
∴∠BMF=∠BAC=60°,∠BFM=∠BCA=60°,
∴∠B=∠BMF=∠BFM=60°,
∴△BMF是等边三角形,
∴FM=BF,∠EMF=120°=∠EAC,
∵EF=EC,
∴∠EFC=∠ECF,
∴∠EFM=180°-60°-∠EFC=120°-∠EFC,∠AEC=180°-60°-∠ECB=120°-∠ECF,
∴∠MFE=∠AEC,
∴△EMF≌△CAE,
∴AE=FM=BF,
∴AE=BF.
(3)结论:FH=3AH.
理由:如图3中,连接AM、FM,在AB上截取AN=BF,连接CN交AF于K,在AF上截取AG=AM,连接GM.
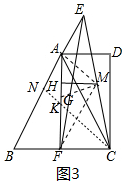
∵AN=BF,AC=AB,∠ABF=∠CAN,
∴△ABF≌△CAN,
∴∠BAF=∠ACN,AF=NC,
∴∠AKN=∠CAK+∠ACN=∠CAK+∠BAF=60°,
∵AE=BF=AN,EM=MC,
∴AM∥NC,AM=
NC=
AF,
∴∠FAM=∠AKN=60°,∵AG=AM,
∴△AGM是等边三角形,
∴AG=GM=AM=
AF,∠AGM=∠AMG=60°,
∴GM=GF,
∴∠GFM=∠GMF=30°,
∴∠AMF=∠AMG+∠GMF=90°,
∵MH⊥AF,
∴∠AHM=90°,∠AMH=30°,
∴AF=2AM,AM=2AH,
∴AF=4AH,
∴FH=3AH.

∵∠BAD=120°,AC平分∠BAD,
∴∠CAB=∠CAD=60°,
∵AD∥BC,
∴∠DAC=∠BCA=60°,
∴∠B=∠BCA=∠BAC=60°,
∴△ABC是等边三角形.
(2)证明:如图2中,作FM∥AC交AB于M.

∵MF∥AC,
∴∠BMF=∠BAC=60°,∠BFM=∠BCA=60°,
∴∠B=∠BMF=∠BFM=60°,
∴△BMF是等边三角形,
∴FM=BF,∠EMF=120°=∠EAC,
∵EF=EC,
∴∠EFC=∠ECF,
∴∠EFM=180°-60°-∠EFC=120°-∠EFC,∠AEC=180°-60°-∠ECB=120°-∠ECF,
∴∠MFE=∠AEC,
∴△EMF≌△CAE,
∴AE=FM=BF,
∴AE=BF.
(3)结论:FH=3AH.
理由:如图3中,连接AM、FM,在AB上截取AN=BF,连接CN交AF于K,在AF上截取AG=AM,连接GM.

∵AN=BF,AC=AB,∠ABF=∠CAN,
∴△ABF≌△CAN,
∴∠BAF=∠ACN,AF=NC,
∴∠AKN=∠CAK+∠ACN=∠CAK+∠BAF=60°,
∵AE=BF=AN,EM=MC,
∴AM∥NC,AM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FAM=∠AKN=60°,∵AG=AM,
∴△AGM是等边三角形,
∴AG=GM=AM=
| 1 |
| 2 |
∴GM=GF,
∴∠GFM=∠GMF=30°,
∴∠AMF=∠AMG+∠GMF=90°,
∵MH⊥AF,
∴∠AHM=90°,∠AMH=30°,
∴AF=2AM,AM=2AH,
∴AF=4AH,
∴FH=3AH.
看了 已知四边形ABCD,AD∥B...的网友还看了以下:
(1)如图1,已知矩形ABCD中,点E是BC上的一动点,过点E作EF⊥BD于点F,EG⊥AC于点G 2020-06-12 …
(2013•瑶海区一模)如图1,在矩形ABCD(AB<BC)的BC边上取一点E,使BA=BE,作∠ 2020-06-12 …
已知:正方形ABCD的边长为6,点E,F分别在边AD,边AB的延长线上,且DE=BF.(1)如图1 2020-06-13 …
已知:如图1,在正方形ABCD,E是BC边上一点,F是CD的中点,且AE=DC+CE.求证:AF平 2020-07-20 …
如图(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交 2020-07-30 …
如图(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交 2020-07-30 …
已知△ABC中,AB=AC,∠BAC=90°,D为BC的中点,AE=CF,连DE、EF.(1)(1) 2020-12-09 …
如图,四边形ABCD是正方形,点G是直线BC上的任意一点,DE⊥AG于点E,BF∥DE,交AG于F. 2020-12-25 …
在△ABC中,已知AB>AC,AD平分∠BAC交BC于点D,点E在DC的延长线上,且DEBD=k,过 2021-01-02 …
如图1,在矩形ABCD(AB<BC)的BC边上取一点E,使BA=BE,作∠AEF=90°,交AD于F 2021-01-16 …