早教吧作业答案频道 -->数学-->
如图,x轴上两个点A(-4,0),B(2,0),直线l经过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
题目详情
如图,x轴上两个点A(-4,0),B(2,0),直线l经过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
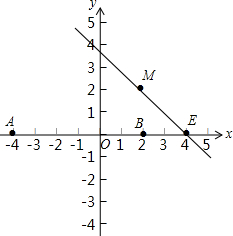
▼优质解答
答案和解析
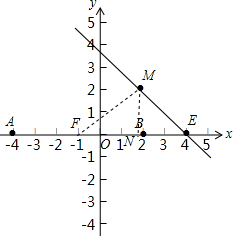 以AB为直径作 F,圆心为F.过E点作 F的切线,这样的切线有2条.
以AB为直径作 F,圆心为F.过E点作 F的切线,这样的切线有2条.
连接FM,过M作MN⊥x轴于点N.
∵A(-4,0),B(2,0),∴F(-1,0), F半径FM=FB=3.
又FE=5,则在Rt△MEF中,
ME=
=4,sin∠MFE=
,cos∠MFE=
.
在Rt△FMN中,MN=MF•sin∠MFE=3×
=12
,
FN=MF•cos∠MFE=3×
=
,则ON=
,
∴M点坐标为(
,
)
直线l过M(
,
),E(4,0),
设直线l的解析式为y=kx+b,则有
,解得
,
所以直线l的解析式为y=-
x+3.
同理,可以求得另一条切线的解析式为y=
x-3.
综上所述,直线l的解析式为y=-
x+3或y=
x-
 以AB为直径作 F,圆心为F.过E点作 F的切线,这样的切线有2条.
以AB为直径作 F,圆心为F.过E点作 F的切线,这样的切线有2条.连接FM,过M作MN⊥x轴于点N.
∵A(-4,0),B(2,0),∴F(-1,0), F半径FM=FB=3.
又FE=5,则在Rt△MEF中,
ME=
| 52-32 |
| 4 |
| 5 |
| 3 |
| 5 |
在Rt△FMN中,MN=MF•sin∠MFE=3×
| 4 |
| 5 |
| 12 |
| 5 |
FN=MF•cos∠MFE=3×
| 3 |
| 5 |
| 9 |
| 5 |
| 4 |
| 5 |
∴M点坐标为(
| 4 |
| 5 |
| 12 |
| 5 |
直线l过M(
| 4 |
| 5 |
| 12 |
| 5 |
设直线l的解析式为y=kx+b,则有
|
|
所以直线l的解析式为y=-
| 3 |
| 4 |
同理,可以求得另一条切线的解析式为y=
| 3 |
| 4 |
综上所述,直线l的解析式为y=-
| 3 |
| 4 |
| 3 |
| 4 |
看了 如图,x轴上两个点A(-4,...的网友还看了以下:
茫然若失写啥的?1.写人物外貌2.写人物神态3.写人物动作4.写景物 2020-04-11 …
一种游艺车,前轮直径0.4米,后轮直径0.3米.前轮转动24周所走的路程,后轮要转多少周?一种游艺 2020-06-03 …
宾语是什么宾语宾语,又称受词,是指一个动作(动词)的接受者.宾语分为直接宾语和间接宾语两大类,其中 2020-07-01 …
不同高度自由下落,同时落地物体沿一条直线作加速运动,从开始计时起,第1秒内的位移是一米,第2秒内的 2020-07-07 …
缩句:1、我绞尽脑汁,终于想出了这道题的答案.2、奥尔加.伊万诺夫娜大步朝我走来.3、她轻轻地做着 2020-07-08 …
已知圆O:x2+y2=4,点P是直线X=4上的动点,若点A(-2,0),B(2,0),直线PA,P 2020-07-30 …
(2005•仙桃)如图,已知直线y=-x+4与x轴、y轴分别交于A、B两点,以OA为直径作半圆,圆心 2020-11-13 …
缩句:1、我绞尽脑汁,终于想出了这道题的答案.2、奥尔加.伊万诺夫娜大步朝我走来.3、她轻轻地做着一 2020-12-09 …
高分乒乓球基础知识试题.1、简述乒乓球直拍和横拍两种握拍方法及各自的特点.2、简述乒乓球运动的基本姿 2020-12-19 …
已知:直线y=4/3x-4与x轴,y轴分别交与点B,C,经过B,C两点的抛物线y=ax²+bx+c与 2021-01-10 …