如图，已知直线AB与正比例函数y=kx（k≠0）的图象交于点A（5，5），与x轴交于点B（-52，0）．点P为直线OA上的动点，点P的横坐标为t，以点P为顶点，作矩形PDEF，满足PD∥x轴，且PD=1，PF=2．（1

Question

如图，已知直线AB与正比例函数y=kx（k≠0）的图象交于点A（5，5），与x轴交于点B（-(5)/(2)，0）．点P为直线OA上的动点，点P的横坐标为t，以点P为顶点，作矩形PDEF，满足PD∥x轴，且PD=1，PF=2．

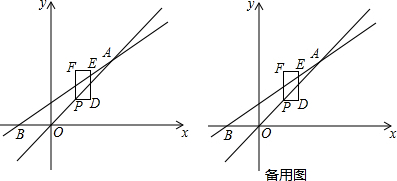
（1）求k值及直线AB的函数表达式；并判定t=1时点E是否落在直线AB上，请说明理由；
（2）在点P运动的过程中，当点F落在直线AB上时，求t的值；
（3）在点P运动的过程中，若矩形PDEF与直线AB有公共点，求t的取值范围．

Answer 1

（1）∵直线AB与正比例函数y=kx（k≠0）的图象交于点A（5，5），与x轴交于点B（-(5)/(2)，0）．
设直线AB的解析式为y=mx+n，
∴5=5k，

5m+n=5

-(5)/(2)m+n=0

，
解得k=1，

m=(2)/(3)

n=(5)/(3)

，
∴直线AB的解析式为y=(2)/(3)x+(5)/(3)；
∵点P为直线OA上的动点，点P的横坐标为t=1，
∴E（2，3），
把x=2，y=3代入y=(2)/(3)x+(5)/(3)中成立，
∴点E落在直线AB上；
（2）∵点P为直线OA上，∴P（t，t），
∴F（t，t+2），
把F（t，t+2）代入y=(2)/(3)x+(5)/(3)中得t+2=(2)/(3)t+(5)/(3)，解得t=-1；
（3）∵P（t，t），
∴D（t+1，t），把D（t+1，t）代入y=(2)/(3)x+(5)/(3)中得t=(2)/(3)（t+1）+(5)/(3)，解得t=7，
∴若矩形PDEF与直线AB有公共点，t的取值范围为-1≤t≤7．