早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的函数表达式;(2)是否存在点P,使得△ACP是以AC为底边的等
题目详情
如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
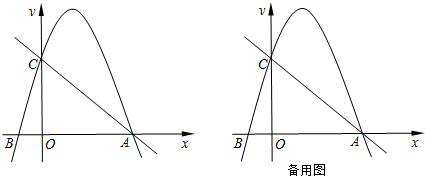
(1)求抛物线的函数表达式;
(2)是否存在点P,使得△ACP是以AC为底边的等腰三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q为线段AC上一点,若四边形OCPQ为平行四边形,求点Q的坐标.

(1)求抛物线的函数表达式;
(2)是否存在点P,使得△ACP是以AC为底边的等腰三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q为线段AC上一点,若四边形OCPQ为平行四边形,求点Q的坐标.
▼优质解答
答案和解析
(1)∵C (0,4),
∴OC=4.
∵OA=OC=4OB,
∴OA=4,OB=1,
∴A (4,0),B (-1,0),
设抛物线解析式:y=a(x+1)(x-4),
∴4=-4a,
∴a=-1.
∴y=-x2+3x+4.
(2)存在.
若△ACP是以AC为底的等腰三角形,则点P在AC的垂直平分线上,
∵OA=OC,
∴AC的垂直平分线OP即为∠AOC的平分线,
设P(m,-m2+3m+4),
则可得:m=-m2+3m+4,
∴m1=
+1,m2=1-
∴存在点P1(
+1,
+1),P2(1-
,1-
),使得△ACP是以AC为底边的等腰三角形.
(3)设lAC:y=kx+b(k≠0),
∵过A (4,0),C (0,4),
∴lAC:y=-x+4.
∵四边形OCPQ为平行四边形,
∴PQ∥OC,PQ=OC,
设P(t,-t2+3t+4),Q(t,-t+4),
-t2+3t+4-(-t+4)=4.
∴t1=t2=2,
∴点Q(2,2).
∴OC=4.
∵OA=OC=4OB,
∴OA=4,OB=1,
∴A (4,0),B (-1,0),
设抛物线解析式:y=a(x+1)(x-4),
∴4=-4a,
∴a=-1.
∴y=-x2+3x+4.
(2)存在.
若△ACP是以AC为底的等腰三角形,则点P在AC的垂直平分线上,
∵OA=OC,
∴AC的垂直平分线OP即为∠AOC的平分线,
设P(m,-m2+3m+4),
则可得:m=-m2+3m+4,
∴m1=
| 5 |
| 5 |
∴存在点P1(
| 5 |
| 5 |
| 5 |
| 5 |
(3)设lAC:y=kx+b(k≠0),
∵过A (4,0),C (0,4),
∴lAC:y=-x+4.
∵四边形OCPQ为平行四边形,
∴PQ∥OC,PQ=OC,
设P(t,-t2+3t+4),Q(t,-t+4),
-t2+3t+4-(-t+4)=4.
∴t1=t2=2,
∴点Q(2,2).
看了 如图,在平面直角坐标系中,已...的网友还看了以下:
(b-c)^2=(c-a)^2=(a-b)^2求证:a=b=c(b-c)^2-(c-a)^2=0( 2020-04-26 …
a,b,c成等差数列,那么证明a^2(b+c),b^2(a+c),c^2(b+c)成等差数列a^2 2020-04-26 …
平行四边形ABCD中ac^2+bd^2=2ab^2类比到平行六面体ABCD-A'B'C'D'是什么 2020-05-13 …
已知a+b+c=0,试求a^2/(2a^2+bc)+b^2/(2b^2+ac)+c^2/(2c^2 2020-06-11 …
网页设计练习题集一、单项选择题1.在HTML中,标记的作用是(C).A.标题标记B.预排版标记C. 2020-06-25 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
整式综合1.求[8+2(k-1)][60-3(k-1)]的最小值.2.已知1/(a-b)+1/(b- 2020-10-31 …
1+a四方小于等于2乘以b-c括号平方,1+b四方小于等于2乘以c-a括号平方,1+c四方小于等于2 2020-11-07 …
乱写乱答求证:A^3+B^3=C^3无整数解的特例设A,B,C互素.A>B,A+B>C,B=2*n1 2020-11-28 …
急求这题高二双曲线题解中的问题!题目:求满足离心率为5/4,虚半轴长为2的双曲线方程及其交点坐标,渐 2020-12-13 …