早教吧作业答案频道 -->数学-->
(1)问题发现小明遇到这样一个问题:如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.小明发现,
题目详情
(1)【问题发现】小明遇到这样一个问题:
如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.小明发现,过点D作DF∥AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系:___;
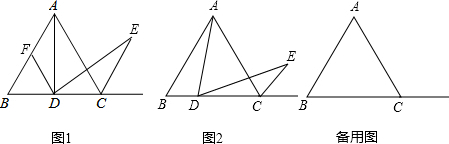
(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件不变),试猜想AD与DE之间的数量关系,并证明你的结论.
(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,请直接写出△ABC与△ADE的面积之比.
如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.小明发现,过点D作DF∥AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系:___;

(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件不变),试猜想AD与DE之间的数量关系,并证明你的结论.
(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,请直接写出△ABC与△ADE的面积之比.
▼优质解答
答案和解析
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°.
又∵DF∥AC,
∴∠BDF=∠BFD=60°,
∴△BDF是等边三角形,
∴DF=BD,∠BFD=60°,
∵BD=CD,
∴DF=CD
∴∠AFD=120°.
∵EC是外角的平分线,
∠DCE=120°=∠AFD,
∵∠ADB=∠ADC=90°,
∴∠ADF=∠ECD=30°,
在△AFD与△EDC中,
,
∴△AFD≌△DCE(ASA),
∴AD=DE;
(2)AD=DE;
证明:如图2,过点D作DF∥AC,交AC于点F,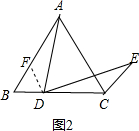
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°,
又∵DF∥AC,
∴∠BDF=∠BFD=60°,
∴△BDF是等边三角形,BF=BD,∠BFD=60°,
∴AF=CD,∠AFD=120°,
∵EC是外角的平分线,
∠DCE=120°=∠AFD,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠FAD=60°+∠FAD,
∵∠ADC=∠ADE+∠EDC=60°+∠EDC,
∴∠ADF=∠EDC,
在△AFD≌△DCE中,
,
∴△AFD≌△DCE(ASA),
∴AD=DE;
(3)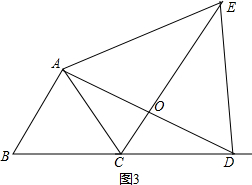 ∵BC=CD,
∵BC=CD,
∴AC=CD,
∵CE平分∠ACD,
∴CE垂直平分AD,
∴AE=DE,
∵∠ADE=60°,
∴△ADE是等边三角形,
∴△ABC∽△ADE,
在Rt△CDO中,
=
,
∴
=
,∴
=
,
∴
=(
∴AB=BC,∠B=∠ACB=∠ABC=60°.
又∵DF∥AC,
∴∠BDF=∠BFD=60°,
∴△BDF是等边三角形,
∴DF=BD,∠BFD=60°,
∵BD=CD,
∴DF=CD
∴∠AFD=120°.
∵EC是外角的平分线,
∠DCE=120°=∠AFD,
∵∠ADB=∠ADC=90°,
∴∠ADF=∠ECD=30°,
在△AFD与△EDC中,
|
∴△AFD≌△DCE(ASA),
∴AD=DE;
(2)AD=DE;
证明:如图2,过点D作DF∥AC,交AC于点F,

∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°,
又∵DF∥AC,
∴∠BDF=∠BFD=60°,
∴△BDF是等边三角形,BF=BD,∠BFD=60°,
∴AF=CD,∠AFD=120°,
∵EC是外角的平分线,
∠DCE=120°=∠AFD,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠FAD=60°+∠FAD,
∵∠ADC=∠ADE+∠EDC=60°+∠EDC,
∴∠ADF=∠EDC,
在△AFD≌△DCE中,
|
∴△AFD≌△DCE(ASA),
∴AD=DE;
(3)
 ∵BC=CD,
∵BC=CD,∴AC=CD,
∵CE平分∠ACD,
∴CE垂直平分AD,
∴AE=DE,
∵∠ADE=60°,
∴△ADE是等边三角形,
∴△ABC∽△ADE,
在Rt△CDO中,
| OD |
| CD |
| ||
| 2 |
∴
| CD |
| AD |
| ||
| 3 |
| AC |
| AD |
| ||
| 3 |
∴
| S△ABC |
| S△ADE |
|
看了 (1)问题发现小明遇到这样一...的网友还看了以下:
事物之间的因果联系,必然具有先行后续的关系,因此[]A.凡是先后出现的现象都具有因果关系B.因果关 2020-05-13 …
当我们说明一个类C实现一个接口I,下面说法()不正确A.接口I是类C一个超类型B.类C也实现了接口 2020-05-17 …
关系模型中,表示实体间N:M联系是通过增加一个(40)。A.关系实现B.属性实现C.关系或一个属性实 2020-05-26 …
如何用C实现一个将整数分解成连续自然数的函数 2020-06-27 …
在暗室里用蜡烛做小孔成像实验时,小明在硬纸板的不同位置上戳了圆形、正三角形、正方形和五角形四个小孔 2020-07-01 …
c++实现一个队列的问题1)加入一个元素到队列(入队IN);2)将一个元素移出队列(出队OUT);3 2020-12-22 …
在暗室里用蜡烛做小孔成像实验时,小明在硬纸板的不同位置上戳了圆形、正三角形、正方形和五角形四个小孔。 2020-12-25 …
如图所示,在静止的木箱内用细绳b、c系住一个小球d,细绳b水平,细绳c与竖直方向成θ角.当系统静止不 2020-12-25 …
如图所示,在静止的木箱内用细绳b、c系住一个小球d,细绳b水平,细绳c与竖直方向成θ角。当系统静止不 2020-12-25 …
如图所示,在静止的木箱内用细绳b、c系住一个小球d,细绳b水平,细绳c与竖直方向成θ角.当系统静止不 2020-12-25 …
 扫描下载二维码
扫描下载二维码