早教吧作业答案频道 -->数学-->
如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和2cm的运动速度同时开始运动
题目详情
如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和2cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动.
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,直线PQ能否把原三角形的周长分成相等的两部分?若能,请求出运动时间;若不能,请说明理由.
(3)在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,直线PQ能否把原三角形的周长分成相等的两部分?若能,请求出运动时间;若不能,请说明理由.
(3)在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.

▼优质解答
答案和解析
(1)如图1,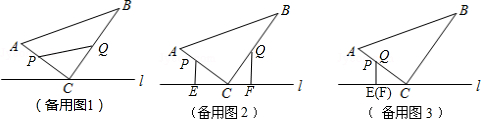
AP=2×1=2(cm),BQ=2×2=4(cm),
CP=6cm-2cm=4cm,CQ=8cm-4cm=4cm
PQ=
=4
(cm);
(2)直线PQ能把原三角形的周长分成相等的两部分,设此时时间为t秒,
理由是:由勾股定理得:AB=
=10(cm),
即△ABC的周长为6cm+8cm+10cm,
∵PQ把△ABC的周长分成相等的两部分,
∴6-t+8-2t=12,
解得:t=
,
即当t=
秒时,直线PQ把原三角形的周长分成相等的两部分;
(3)如图2,
∵△PEC与△QFC全等,
∴PC=QC.
∴6-t=8-2t.
解得:t=2;
如图3,
∵点P与点Q重合,
∴△PEC与△QFC全等,
∴6-t=2t-8.
解得:t=
.
综上所述:点P运动时间为2秒或
秒时,△PEC与△QFC全等.

AP=2×1=2(cm),BQ=2×2=4(cm),
CP=6cm-2cm=4cm,CQ=8cm-4cm=4cm
PQ=
| 42+42 |
| 2 |
(2)直线PQ能把原三角形的周长分成相等的两部分,设此时时间为t秒,
理由是:由勾股定理得:AB=
| 62+82 |
即△ABC的周长为6cm+8cm+10cm,
∵PQ把△ABC的周长分成相等的两部分,
∴6-t+8-2t=12,
解得:t=
| 2 |
| 3 |
即当t=
| 2 |
| 3 |
(3)如图2,
∵△PEC与△QFC全等,
∴PC=QC.
∴6-t=8-2t.
解得:t=2;
如图3,
∵点P与点Q重合,
∴△PEC与△QFC全等,
∴6-t=2t-8.
解得:t=
| 14 |
| 3 |
综上所述:点P运动时间为2秒或
| 14 |
| 3 |
看了 如图,△ABC中,∠ACB=...的网友还看了以下:
在直角梯形ABCD中,AD∥BC,∠C=90度,BC=16,AD=21,DC=12,动点P从点D出 2020-05-01 …
如图1,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D是BC上一定点.动点P从C 2020-06-12 …
如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的 2020-06-15 …
如图,在长方形ABCD中,AB=120厘米,点P以2厘米/秒的速度从A到B匀速运动.点Q以3厘米/ 2020-07-08 …
如图,四边形ABCD是边长为4的正方形,动点P、Q同时从A点出发,点P沿AB以每秒1个单位长度的速 2020-07-09 …
如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从 2020-07-17 …
如图所示,在射线OM上有三点A、B、C.OA=20,AB=m,BC=n,m,n满足|m-6n|=- 2020-07-24 …
关于打点计时器打出的纸带,下列叙述中正确的是()A.点迹均匀,说明纸带做匀速运动B.点迹变稀,说明纸 2020-11-10 …
(本题满分10分)如图1,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D是BC上一 2020-12-13 …
(2014•绥化)如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A 2021-01-16 …