早教吧作业答案频道 -->数学-->
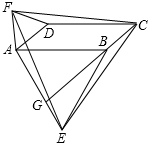
如图,在▱ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:①CG⊥AE;②△CDF≌△EBC;③∠CDF=∠EAF;④△ECF是等边三角形
题目详情
如图,在▱ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:
①CG⊥AE;
②△CDF≌△EBC;
③∠CDF=∠EAF;
④△ECF是等边三角形.
其中一定正确的是___.(把正确结论的序号都填上)
①CG⊥AE;
②△CDF≌△EBC;
③∠CDF=∠EAF;
④△ECF是等边三角形.
其中一定正确的是___.(把正确结论的序号都填上)

▼优质解答
答案和解析
在等边三角形ABE中,
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段
∴如果CG⊥AE,则G是AE的中点,∠ABG=30°,∠ABC=150°,题目缺少这个条件,CG⊥AE不能求证,故①错误;
∵△ABE、△ADF是等边三角形
∴FD=AD,BE=AB
∵AD=BC,AB=DC
∴FD=BC,BE=DC
∵∠B=∠D,∠FDA=∠ABE
∴∠CDF=∠EBC
∴△CDF≌△EBC,故②正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°-∠CDA)=300°-∠CDA,
∠FDC=360°-∠FDA-∠ADC=300°-∠CDA,
∴∠CDF=∠EAF,故③正确;
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC,
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故④正确;
正确的有②③④,
故答案为:②③④.
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段
∴如果CG⊥AE,则G是AE的中点,∠ABG=30°,∠ABC=150°,题目缺少这个条件,CG⊥AE不能求证,故①错误;
∵△ABE、△ADF是等边三角形
∴FD=AD,BE=AB
∵AD=BC,AB=DC
∴FD=BC,BE=DC
∵∠B=∠D,∠FDA=∠ABE
∴∠CDF=∠EBC

∴△CDF≌△EBC,故②正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°-∠CDA)=300°-∠CDA,
∠FDC=360°-∠FDA-∠ADC=300°-∠CDA,
∴∠CDF=∠EAF,故③正确;
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC,
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故④正确;
正确的有②③④,
故答案为:②③④.
看了 如图,在▱ABCD中,分别以...的网友还看了以下:
网络测试不能解决的问题是______。A.连通性B.丢包C.全表扫描D.延迟A.B.C.D. 2020-05-26 …
标况下,m克气体A与n克气体B分子数相同,下列说法不正确的是()A.两气体的相对分子质量比为m:n 2020-06-18 …
不知有否人能看懂...一道数学计算题~这题很扯...计算:(a+b)的平方倍的根号下16/a+b+ 2020-06-24 …
什么情况下a+b的最小值是"根号下2ab"?我知道a>0,b>0,当取到等号时a=b.我们都知道正 2020-07-19 …
把(a-b)倍根号下-1/a-b化成最简二次根式,正确的结果是()(A)根号下b-a(B)根号下a 2020-08-02 …
贺龙的革命事迹有①任南昌起义代总指挥②开创湘鄂西农村革命根据地③开创晋绥抗日根据地④1948年参与指 2020-11-13 …
下列历史事件按时间先后顺序排列正确的是①刘邓大军强渡黄河,发动进攻②开辟大别山根据地③国民党军队进攻 2020-11-13 …
数学问题,紧急求援!设等式根号下a(b-a)+根号下a(c-a)=根号下b-a-根号下a-c在实数范 2020-12-31 …
已知线段a,b,延长a,b到c,使b,c=三分之一a,b.d为a,c的中点,若d,c=5cm,求a, 2021-01-02 …
这些等式成立吗?——a方+b方=(a+b)方a方乘以b方=(ab)方√a+√b=根号下a+b根号下( 2021-01-22 …