早教吧作业答案频道 -->数学-->
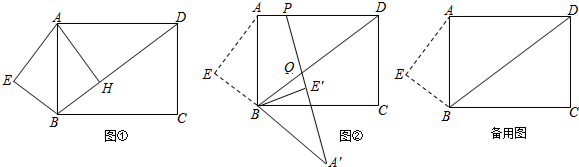
已知:如图①,在矩形ABCD中,AB=5,AD=203.过A作AH⊥BD于H.(1)将△AHB沿AB翻折,得△AEB.求证:∠EAB=∠ADB;(2)如图②,将△ABE绕点B顺时针旋转,记旋转中的△ABE为△A′BE′,在旋转过
题目详情
已知:如图①,在矩形ABCD中,AB=5,AD=
.过A作AH⊥BD于H.
(1)将△AHB沿AB翻折,得△AEB.求证:∠EAB=∠ADB;
(2)如图②,将△ABE绕点B顺时针旋转,记旋转中的△ABE为△A′BE′,在旋转过程中,延长A′E′与对角线BD交于点Q,与边AD交于点P,问是否存在这样的Q、P两点,使△DQP为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
| 20 |
| 3 |
(1)将△AHB沿AB翻折,得△AEB.求证:∠EAB=∠ADB;
(2)如图②,将△ABE绕点B顺时针旋转,记旋转中的△ABE为△A′BE′,在旋转过程中,延长A′E′与对角线BD交于点Q,与边AD交于点P,问是否存在这样的Q、P两点,使△DQP为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.

▼优质解答
答案和解析
(1)证明:由翻折可知:∠EAB=∠BAH.
∵∠BAH+∠DAH=∠DAH+∠ADB=90°.
∴∠BAH=∠ADB,
∴∠EAB=∠ADB.
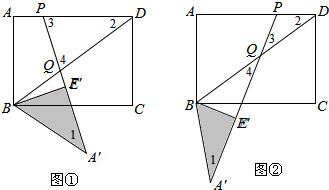
(2)如图①所示,当PD=DQ时,
 ∵∠1=∠2,
∵∠1=∠2,
∴∠A′BQ=∠A′QB,
∴A′Q=A′B=5,
∴E′Q=1.
在Rt△E′BQ中,BQ=
=
.
∴DQ=
-
.
如图②所示,当PQ=PD,
由∠1=∠2可得∠1=∠4,
∴BQ=A′B=5,
∴DQ=BD-BQ=
-5=
.
当QP=QD时,点P不在AD上,不合题意.
综上可知:当DQ=
-
或
时,△DPQ是等腰三角形.
∵∠BAH+∠DAH=∠DAH+∠ADB=90°.
∴∠BAH=∠ADB,
∴∠EAB=∠ADB.
(2)如图①所示,当PD=DQ时,
 ∵∠1=∠2,
∵∠1=∠2,∴∠A′BQ=∠A′QB,
∴A′Q=A′B=5,
∴E′Q=1.
在Rt△E′BQ中,BQ=
| E′B2+E′Q2 |
| 10 |
∴DQ=
| 25 |
| 3 |
| 10 |
如图②所示,当PQ=PD,
由∠1=∠2可得∠1=∠4,
∴BQ=A′B=5,
∴DQ=BD-BQ=
| 25 |
| 3 |
| 10 |
| 3 |
当QP=QD时,点P不在AD上,不合题意.
综上可知:当DQ=
| 25 |
| 3 |
| 10 |
| 10 |
| 3 |
看了 已知:如图①,在矩形ABCD...的网友还看了以下:
两条互相平行的直线分别过点A(6,2)和B(-3,-1)并且绕着A,B旋转 如果这两条直线间距离为 2020-05-13 …
电流互感器的故障多由( )造成的。A.次级绕组开路B.次级绕组短路C.次级绕组接地D.初级绕组短路 2020-05-28 …
下列现象中,与分子热运动有关的是()A.尘土飞扬B.烟雾缭绕C.臭气熏天D.余下列现象中,与分子热 2020-07-02 …
牵牛花、竹子、黄瓜、西瓜它们的茎分别是()A.匍匐茎、缠绕茎、直立茎、攀缘茎B.缠绕茎、直立茎、攀 2020-07-07 …
下列结论中,正确的是()A.三角形绕其一边旋转一周后成一个圆锥B.一个直角梯形绕其一边旋转一周后成 2020-07-25 …
我们看到的日月星辰东升西落是因为()A.地球绕太阳自西向东公转B.地球绕太阳自东向西公转C.地球绕 2020-07-25 …
一次函数旋转问题已知一次函数y=2x+4求1)绕点(0,1)顺时针旋转90°后的解析式1)绕点(1 2020-08-01 …
漆包线重量?1、绕线的模具(圆形)Ф20×0.18mm(绕出来的线圈内径是Ф20mm,厚度是0.18 2020-11-18 …
2007年我国发射了“嫦娥”1号绕月飞船,“嫦娥”1号飞船发射后先绕地球运转,经多次变轨后进入月球轨 2020-12-15 …
1.环绕亚洲大陆的邻居有()A欧洲B非洲C南极洲D大洋州2.把下列亚洲的河流与其注入的海洋正确排列( 2020-12-22 …