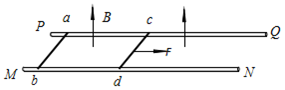
如图所示，PQ和MN是固定于水平面内的平行光滑金属轨道，轨道足够长，其电阻可忽略不计．金属棒ab、cd放在轨道上，始终与轨道垂直，且接触良好．金属棒ab、cd的质量均为m，长度均为L．

Question

如图所示，PQ和MN是固定于水平面内的平行光滑金属轨道，轨道足够长，其电阻可忽略不计．金属棒ab、cd放在轨道上，始终与轨道垂直，且接触良好．金属棒ab、cd的质量均为m，长度均为L．两金属棒的长度恰好等于轨道的间距，它们与轨道形成闭合回路．金属棒ab的电阻为2R，金属棒cd的电阻为R．整个装置处在竖直向上、磁感应强度为B的匀强磁场中．
若先保持金属棒ab不动，使金属棒cd在与其垂直的水平力F（大小未知）作用下，由静止开始向右以加速度a做匀加速直线运动，水平力F作用t₀时间撤去此力，同时释放金属棒ab．求：

（1）棒cd匀加速过程中，外力F随时间变化的函数关系；
（2）两金属棒在撤去F后的运动过程中，直到最后达到稳定，金属棒ab产生的热量；
（3）两金属棒在撤去F后的运动过程中，直到最后达到稳定，通过金属棒cd的电荷量q．

Answer 1

（1）棒cd匀加速过程中，水平方向上只受F和安培力F'的作用，F′=BIL=B•(BLv)/(R+2R)•L=(B2L2a)/(3R)t，所以F=F′+ma=(B2L2a)/(3R)t+ma；
（2）金属棒cd撤去外力时的速度v=at₀；
在撤去外力后，金属棒ab，cd在水平方向上只受安培力的作用，且两棒的安培力大小相等，方向相反；
最终达到稳定状态时，两金属棒之间的磁通量不再发生改变，即两棒的速度相等，设都为v'，
将两棒当成一个整体，则在水平方向上，合外力为零，利用动量守恒定律则有：mv=mv'+mv'；
所以，v′=(1)/(2)v=(1)/(2)at0；
对整个过程应用动能定理，则金属棒总共产生的热量Q等于克服安培力所做的功=(1)/(2)mv2-(1)/(2)mv′2-(1)/(2)mv′2=(1)/(4)mv2=(1)/(4)ma2t02；
在整个过程中，通过金属棒ab，cd的电流相等，所以，金属棒ab产生的热量=(2R)/(2R+R)Q=(1)/(6)ma2t02；
（3）两金属棒在撤去F后的运动过程中，直到最后达到稳定过程中，在一极短时间段△t内对金属棒cd应用动量守恒定理，则有：
F'•△t=BIL•△t=BL△q=-m△v，
因为上式对任一极短时间都成立，那么对整个过程则有：BLq=-m(v′-v)=(1)/(2)mv，
所以，q=((1)/(2)mv)/(BL)=(mat0)/(2BL)．
答：（1）棒cd匀加速过程中，外力F随时间变化的函数关系为F=(B2L2a)/(3R)t+ma；
（2）两金属棒在撤去F后的运动过程中，直到最后达到稳定，金属棒ab产生的热量为(1)/(6)ma2t02；
（3）两金属棒在撤去F后的运动过程中，直到最后达到稳定，通过金属棒cd的电荷量q为(mat0)/(2BL)．