已知函数f(x)=|lg(-x)|,x<0x2-6x+4,x≥0,若关于x的方程f2(x)-bf(x)+1=0有8个不同根,则实数b的取值范围是()A.(2,174]B.(2,174]∪(-∞,-2)C.(2,8)D.(-∞,-2)∪(2,+
已知函数f(x)=
,若关于x的方程f2(x)-bf(x)+1=0有8个不同根,则实数b的取值范围是( )|lg(-x)|,x<0 x2-6x+4,x≥0
A. (2,
]17 4
B. (2,
]∪(-∞,-2)17 4
C. (2,8)
D. (-∞,-2)∪(2,+∞)
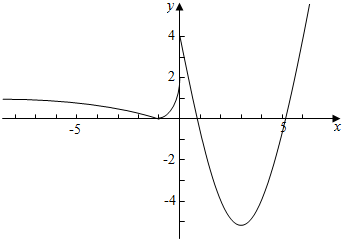
∵关于x的函数y=f2(x)-bf(x)+1有8个不同的零点,
∴方程x2-bx+1=0有2个不同的正解,且在(0,4]上;
∴
|
解得,2<b≤
| 17 |
| 4 |
故选:A.
(1)x/a+x/b-a+a/a+b(a不等于0,axa不等于bxb)(2)(mx-n)(m+n) 2020-04-07 …
Matlab出现isnotavalidexpressionorequation.clear;sym 2020-04-26 …
已知a,b,c成等比数列,如果a,x,b和b,y,c都成等差数列,则a/x + c/y=?下面是某 2020-05-16 …
集合题不懂,设Z为整数集合,A={x|x∈Z,x>x},B={x|x∈Z,x≠x},则(A)A=B 2020-06-18 …
2.对任意实数X,点P(x,x²-2x)一定不在第几象3.已知点A﹙2a+3b,﹣2﹚和点B﹙8, 2020-06-20 …
高中函数题:设f(x)=x/e^x,a≠b,f(a)=f(b),比较a+b与2的大小我是这么想的但 2020-07-13 …
8:x=10:622分之21:8分之x=7:122.7:5.4=x:31.8:x=0.2:0.12 2020-07-18 …
1.7/x²-1+8/x²-2x=37-9x/x^3-x²-x+12.3/x²+x-2=x/x-1 2020-07-18 …
已知函数f(x)=(|x|-b)2+c,函数g(x)=x+m,(1)当b=2,m=-4时,f(x) 2020-07-31 …
1.设函数F(X)=X^2+X-(1/4),若定义域为[a,a+1],值域为[-0.5,1/16], 2020-10-31 …