早教吧作业答案频道 -->数学-->
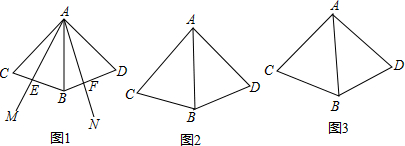
如图1,以AB为腰向两侧分别作全等的等腰△ABC和△ABD,过点A作∠MAN,使∠MAN=∠BAC=α(0°<α<60°),将∠MAN的边AM与AC叠合,绕点A按逆时针方向旋转,与射线CB,BD分别交于点E,F,设旋转
题目详情
如图1,以AB为腰向两侧分别作全等的等腰△ABC和△ABD,过点A作∠MAN,使∠MAN=∠BAC=α(0°<α<60°),将∠MAN的边AM与AC叠合,绕点A按逆时针方向旋转,与射线CB,BD分别交于点E,F,设旋转角度为β.
(1)如图1,当0°<β<α时,线段BE与DF相等吗?请说明理由.
(2)当α<β<2α时,线段CE,FD与线段BD具有怎样的数量关系?请在图2中画出图形并说明理由.
(3)联结EF,在∠MAN绕点A逆时针旋转过程中(0°<β<2α),当线段AD⊥EF时,请用含α的代数式直接表示出∠CEA的度数.
(1)如图1,当0°<β<α时,线段BE与DF相等吗?请说明理由.
(2)当α<β<2α时,线段CE,FD与线段BD具有怎样的数量关系?请在图2中画出图形并说明理由.
(3)联结EF,在∠MAN绕点A逆时针旋转过程中(0°<β<2α),当线段AD⊥EF时,请用含α的代数式直接表示出∠CEA的度数.

▼优质解答
答案和解析
(1)结论:BE=DF.
理由:如图1中,
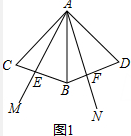
∵等腰△ABC和△ABD全等,
∴AB=AC=AD,∠C=∠ABC=∠ABD=∠D,∠BAC=∠BAD,
∵∠MAN=∠BAC=α,
∴∠MAN=∠BAD=α,
∴∠EAB=∠FAD,
在△AEB和△AFD中,
,
∴△AEB≌△AFD,
∴BE=DF.
(2)结论:CE-FD=BD.
理由:如图2中所示,∵∠MAN=∠BAD,
∴∠DAF=∠BAE,
∵∠ABC=∠ADB,
∴∠ABE=∠ADF,
在△ABE和△ADF中,
,
∴△AEB≌△AFD,
∴BE=DF,
∵BC=BD,
∴CE-FD=CE-BE=BC=BD.
(3)结论:90°-α.
理由:如图3中,AE交BD于点O.
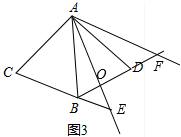
∵AD⊥EF,
∴∠DAF+∠AFE=90°,
∵∠DAF=∠BAE,∠ABD=∠AFE,
∴∠OAB+∠OBA=90°,
∴∠AOB=∠AOF=90°,
∴∠AFD=90°-∠EAF=90°-α,
∵∠CEA=∠AFD,
∴∠CEA=90°-α.
理由:如图1中,

∵等腰△ABC和△ABD全等,
∴AB=AC=AD,∠C=∠ABC=∠ABD=∠D,∠BAC=∠BAD,
∵∠MAN=∠BAC=α,
∴∠MAN=∠BAD=α,
∴∠EAB=∠FAD,
在△AEB和△AFD中,
|
∴△AEB≌△AFD,
∴BE=DF.
(2)结论:CE-FD=BD.
理由:如图2中所示,∵∠MAN=∠BAD,
∴∠DAF=∠BAE,
∵∠ABC=∠ADB,
∴∠ABE=∠ADF,
在△ABE和△ADF中,
|
∴△AEB≌△AFD,
∴BE=DF,
∵BC=BD,
∴CE-FD=CE-BE=BC=BD.
(3)结论:90°-α.
理由:如图3中,AE交BD于点O.

∵AD⊥EF,
∴∠DAF+∠AFE=90°,
∵∠DAF=∠BAE,∠ABD=∠AFE,
∴∠OAB+∠OBA=90°,
∴∠AOB=∠AOF=90°,
∴∠AFD=90°-∠EAF=90°-α,
∵∠CEA=∠AFD,
∴∠CEA=90°-α.
看了 如图1,以AB为腰向两侧分别...的网友还看了以下:
岸两边有A,B两点,求M,N使AM+MN+NB最短桥的选址问题:河的两岸分别有A,B两点,两岸平行 2020-04-06 …
这是一个具有一定的排列规律的三角形数垒,a,b是第n行的前两个数,当n=8时,a=?b=?这是一个 2020-06-25 …
设m、n是两条不同的直线,α,β是两个不同的平面,则m⊥α的一个充分条件是()A.m∥n,n∥β, 2020-07-13 …
如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的 2020-07-18 …
悖论:为什么这样不能证明任何大于二的偶数可以表示为两个素数和任意两素数差为偶数b-a=2m,m∈Z 2020-07-24 …
若a大于b大于0,那么a的n次方大于b的n次方.为什么不等式两边含绝对值能平方去绝对值不等式这一章 2020-07-30 …
如图所示,小磁针处于静止状态,由此判断a、b两磁极的磁性是()A.a为N极,b为S极B.a为S极,b 2020-11-01 …
如图所示,将甲图的条形磁铁从中间锯断,如乙图所示,则下列关于乙图的说法中正确的是()。A.a端是N极 2020-11-01 …
平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b 2020-11-03 …
平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b 2020-11-03 …