早教吧作业答案频道 -->数学-->
如图1,在等腰Rt△ACB中,∠ACB=90°,AC=BC;在等腰Rt△DCE中,∠DCE=90°,CD=CE;点D、E分别在边BC、AC上,连接AD、BE,点N是线段BE的中点,连接CN与AD交于点G.(1)若CN=6.5,CE=5,求BD的值.(2)
题目详情
如图1,在等腰Rt△ACB中,∠ACB=90°,AC=BC;在等腰Rt△DCE中,∠DCE=90°,CD=CE;点D、E分别在边BC、AC上,连接AD、BE,点N是线段BE的中点,连接CN与AD交于点G.
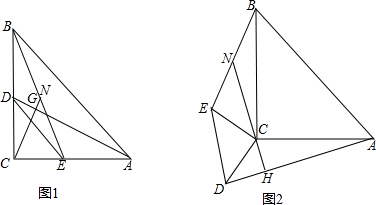
(1)若CN=6.5,CE=5,求BD的值.
(2)求证:CN⊥AD.
(3)把等腰Rt△DCE绕点C转至如图2位置,点N是线段BE的中点,延长NC交AD于点H,请问(2)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.

(1)若CN=6.5,CE=5,求BD的值.
(2)求证:CN⊥AD.
(3)把等腰Rt△DCE绕点C转至如图2位置,点N是线段BE的中点,延长NC交AD于点H,请问(2)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
▼优质解答
答案和解析
(1)∵∠ACB=90°,点N是线段BE的中点,
∴BE=2CN=13,
∵CE=5,
∴BC=
=12,
∵CD=CE=5,
∴BD=BC-CD=7;
(2)在△ACD与△BCE中,
,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ACB=90°,点N是线段BE的中点,
∴CN=BN,
∴∠CBE=∠NCD,
∴∠NCD=∠CAD,
∵∠NCD+∠NCA=90°,
∴∠CAG+∠GCA=90°,
∴∠CGA=90°,
∴CN⊥AD;
(3)(2)中的结论还成立,如图2,延长CN到F使FN=CN,连接BF,
在△CEN与△BFN中,
,
∴△CEN≌△BNF,
∴CE=BF,∠F=∠ECN,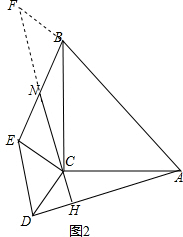
∵∠CBF=180°-∠F-∠BCF,∠DCA=360°-∠DCE-∠ACB-∠BCE=180°-∠ECF-∠BCF,
∴∠CBF=∠DCA,
∵CE=CD,
∴BF=CD,
在△ACD与△BCF中,
,
∴△ACD≌△BCF,
∴∠DAC=∠BCF,
∵∠BCF+∠ACH=90°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,
∴CN⊥AD.
∴BE=2CN=13,
∵CE=5,
∴BC=
| BE2-CE2 |
∵CD=CE=5,
∴BD=BC-CD=7;
(2)在△ACD与△BCE中,
|
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ACB=90°,点N是线段BE的中点,
∴CN=BN,
∴∠CBE=∠NCD,
∴∠NCD=∠CAD,
∵∠NCD+∠NCA=90°,
∴∠CAG+∠GCA=90°,
∴∠CGA=90°,
∴CN⊥AD;
(3)(2)中的结论还成立,如图2,延长CN到F使FN=CN,连接BF,
在△CEN与△BFN中,
|
∴△CEN≌△BNF,
∴CE=BF,∠F=∠ECN,

∵∠CBF=180°-∠F-∠BCF,∠DCA=360°-∠DCE-∠ACB-∠BCE=180°-∠ECF-∠BCF,
∴∠CBF=∠DCA,
∵CE=CD,
∴BF=CD,
在△ACD与△BCF中,
|
∴△ACD≌△BCF,
∴∠DAC=∠BCF,
∵∠BCF+∠ACH=90°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,
∴CN⊥AD.
看了 如图1,在等腰Rt△ACB中...的网友还看了以下:
已知a.b.c分别是三角形ABC的三个内角A.B.C所对的边,若三角形ABC面积S三角形ABC=2 2020-04-05 …
学生的评分标准A,A+,B,B+,C,C+……分别表示什么?A,A+,B,B+,C,C+……分别表 2020-04-26 …
高中数学懂得进,急啊,完了追加10填空:在三角形ABC中,已知a=1,A=六分之派,则(sinA+ 2020-05-16 …
三个班的代表队进行N(N≥2)次篮班比赛,每次第一名得a分,第二名得b分,第三名得c分(a、b、c 2020-06-13 …
肾小球滤过率是指()A.两侧肾脏每分钟生成的原尿量与肾血浆流量之比B.一侧肾脏每分钟生成的原尿量C 2020-07-01 …
知|a|=2,|b|=3,a与b异号,求|a­­‐b|的值已知|a-2分之1|+| 2020-07-30 …
在三角形ABC中,AB=1,BC=2,求角C的取值范围题目做到最后一步,说的是当x=根号3时,co 2020-07-30 …
在三角形ABC中,a,b,c分别为角A,B,C所对的边长,且a=3,A=派/3,点D在BC边上.(一 2020-11-02 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
如图1,有两个分别涂有黄色和蓝色的Rt△ABC和Rt△A′B′C′,其中∠C=∠C′=90°,∠A= 2020-12-25 …