早教吧作业答案频道 -->数学-->
在等边△ABC中,边AB=2cm,点D是边BC的中点,点E是从点B沿B→A→C的方向开始运动的一个动点,速度为1cm/s,当E点运动t秒时,(1)当△BED是直角三角形时,求t的值;(2)当DE将△ABC的周长分
题目详情
在等边△ABC中,边AB=2cm,点D是边BC的中点,点E是从点B沿B→A→C的方向开始运动的一个动点,速度为1cm/s,当E点运动t秒时,
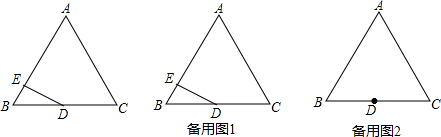
(1)当△BED是直角三角形时,求t的值;
(2)当DE将△ABC的周长分成的两部分之间是2倍的关系时,求t的值;
(3)当点E只在边AC上运动时,是否存在一点E使得DE+BE的值取得最小值?如果不存在,请说明理由;如果存在,请直接写出此时DE+BE的最小值(不要求写过程).

(1)当△BED是直角三角形时,求t的值;
(2)当DE将△ABC的周长分成的两部分之间是2倍的关系时,求t的值;
(3)当点E只在边AC上运动时,是否存在一点E使得DE+BE的值取得最小值?如果不存在,请说明理由;如果存在,请直接写出此时DE+BE的最小值(不要求写过程).
▼优质解答
答案和解析
(1)分两种情况:
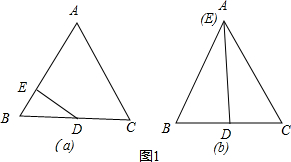
当∠BED=90°时,
如图1,∵△ABC是等边三角形,
∴∠B=60°,
∴∠BDE=30°,
∴BE=
BD,
∵AB=AC=BC=2cm,BD=CD=
BC=
×2=1cm,
∴BE=
cm,
∴t=
秒;
当∠BDE=90°时,
∵△ABC是等边三角形,BD=DC,
∴E与A重合,
∴BE=AB=2cm.
∴t=2秒
(2)分两种情况:
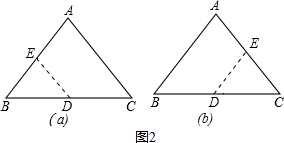
E点在AB上时,如图,
∵AB=AC=2cm,BD=CD=
BC=
×2=1cm,
设E点运动了t秒,则BE=t,AE=2-t,由题意得:
BE+BD=
(AE+AC+CD),
∴t+1=
(2-t+2+1),
解得t=1秒;
E点在AC上时,如图,
∵AB=AC=BC=2cm,BD=CD=
BC=
×2=1cm,E点运动了t秒,
则AB+AE=t,EC=AB+AC-t=4-t,
由题意得:BD+AB+AE=2(EC+CD),
∴1+t=2(4-t+1),
解得t=3秒.
故当t=1或3秒时,DE把△ABC的周长分成的两部分之间是2倍的关系.
(3)作B关于AC的对称点B′,然后连接BD交AC于E,即为所求;此时DE+BE=B′D;
作BG⊥BC于G,
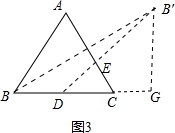
∴△ABC是等边三角形,BC=2,
∴∠B′BC=30°,B′B=2
,
∴B′G=
,BG=3,
∵BD=CD=1,
∴DG=2,
在RT△B′GD中,B′D=
=
.
∴DE+BE的最小值=
.

当∠BED=90°时,
如图1,∵△ABC是等边三角形,
∴∠B=60°,
∴∠BDE=30°,
∴BE=
| 1 |
| 2 |
∵AB=AC=BC=2cm,BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=
| 1 |
| 2 |
∴t=
| 1 |
| 2 |
当∠BDE=90°时,
∵△ABC是等边三角形,BD=DC,
∴E与A重合,
∴BE=AB=2cm.
∴t=2秒
(2)分两种情况:

E点在AB上时,如图,
∵AB=AC=2cm,BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
设E点运动了t秒,则BE=t,AE=2-t,由题意得:
BE+BD=
| 1 |
| 2 |
∴t+1=
| 1 |
| 2 |
解得t=1秒;
E点在AC上时,如图,
∵AB=AC=BC=2cm,BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
则AB+AE=t,EC=AB+AC-t=4-t,
由题意得:BD+AB+AE=2(EC+CD),
∴1+t=2(4-t+1),
解得t=3秒.
故当t=1或3秒时,DE把△ABC的周长分成的两部分之间是2倍的关系.
(3)作B关于AC的对称点B′,然后连接BD交AC于E,即为所求;此时DE+BE=B′D;
作BG⊥BC于G,

∴△ABC是等边三角形,BC=2,
∴∠B′BC=30°,B′B=2
| 3 |
∴B′G=
| 3 |
∵BD=CD=1,
∴DG=2,
在RT△B′GD中,B′D=
| DG2+B′G2 |
| 7 |
∴DE+BE的最小值=
| 7 |
看了 在等边△ABC中,边AB=2...的网友还看了以下:
设直线L1的倾斜角为α,α∈(0,π2),L1绕其上一点P沿逆时针方向旋转α角得到直线L2,L2的 2020-05-16 …
设直线L1的倾斜角为α,α∈(0,π2),L1绕其上一点P沿逆时针方向旋转α角得到直线L2,L2的 2020-06-03 …
已知对任意平面向量AB=(x,y),把AB绕其起点沿逆时针方向旋转θ角得到向量AP=(xcosθ- 2020-06-14 …
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于 2020-06-20 …
如图,已知中,AB=AC把绕A点沿顺时针方向旋转得到连接BDCE交于点F.(1)求证:;(2)若A 2020-06-20 …
高中数学题已知对任意平面向量向量AB=(x,y),把向量AB绕其起点沿逆时针方向旋转角a得到向量A 2020-06-22 …
已知对任意平面向量AB=(x,y),把AB绕其起点沿逆时针方向旋转θ角得到向量:AP=(xcosθ 2020-07-31 …
如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N,证明:(1)B 2020-08-03 …
如图1中△ABC和△ADE都是等腰直角三角形,∠ACB=∠D=90°,点C在AE上,△ABC绕着A点 2020-11-01 …
试试你的作图能力(1)将下列图中的三角形绕O点沿逆时针旋转90°,再向右平移5格.(2)在数轴上作出 2020-11-06 …