早教吧作业答案频道 -->数学-->
如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.(1)求证:ED=BD;(2)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长.
题目详情
如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
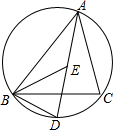
(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长.

(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长.
▼优质解答
答案和解析
(1)证明:∵点E是△ABC的内心,
∴∠BAD=∠CAD,∠ABE=∠CBE,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BED=∠ABE+∠BAD,
∴∠ABE=∠CBE,∠BAD=∠CAD=∠CBD,
∵∠EBD=∠CBE+∠CBD,
∴∠BED=∠EBD,
∴ED=BD;
(2) 连接CD,
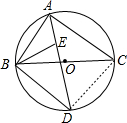
∵∠BAC=90°,
∴BC是 O的直径,
∴∠BDC=90°,
∵ O的直径=6,
∴BC=6,
∵E为△ABC的内切圆的圆心,
∴∠BAD=∠CAD,
∴BD=DC,
∴BD=DC=
BC=3
.
∴∠BAD=∠CAD,∠ABE=∠CBE,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BED=∠ABE+∠BAD,
∴∠ABE=∠CBE,∠BAD=∠CAD=∠CBD,
∵∠EBD=∠CBE+∠CBD,
∴∠BED=∠EBD,
∴ED=BD;
(2) 连接CD,

∵∠BAC=90°,
∴BC是 O的直径,
∴∠BDC=90°,
∵ O的直径=6,
∴BC=6,
∵E为△ABC的内切圆的圆心,
∴∠BAD=∠CAD,
∴BD=DC,
∴BD=DC=
| ||
| 2 |
| 2 |
看了 如图,点E是△ABC的内心,...的网友还看了以下:
研究人员用X射线照射细菌菌落A,四个小时后,发现菌落A中产生了a1、a2两个突变种.研究人员用菌种 2020-05-17 …
(9分)下面有关细菌A的四项实验,分析并回答相关问题:实验1:将细菌A接种于基本培养基(能满足野生 2020-05-17 …
(07郑州市三检)(19分)用放射线处理细菌A,产生a1、a2两个突变种。下列是四项与之有关的实验 2020-05-17 …
有联接点O(0,0)和点A(1,1)一段向上凸的曲线弧OA,对于OA上任一点P(x,y)曲线OP与 2020-05-17 …
关于JAVA接口假设:接口A有方法a,b,c,d,接口B有方法d,e,f,g。1.若类C实现A接口 2020-05-17 …
在直角坐标系中,M为x轴正半轴上一点,⊙M交x轴于A、B两点,交y轴于C、D两点,P为AB延长线上 2020-05-17 …
已知焦点在x轴上的椭圆方程为x24a+y2a2-1=1,随着a的增大该椭圆的形状()A.越接近于圆 2020-06-27 …
对于线性相关系数,叙述正确的是()A.|r|≤1,|r|越接近于1,相关程度越弱,|r|越接近于0 2020-08-02 …
1.试写出a(n+1)于an的关系,并证明{a(n+1)-4/5}是等比数列.2.问至少要经过多少年 2020-11-04 …
(2006•攀枝花)如图所示,要使灯L1和L2串联,则关于1、2、3、4四个接线柱的连接,正确的是( 2020-11-12 …