早教吧作业答案频道 -->数学-->
如图1,在△ABC中,BC=4,以线段AB为边作△ABD,使得AD=BD,连接DC,再以DC为边作△CDE,使得DC=DE,∠CDE=∠ADB=α.(1)如图2,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;(2
题目详情
如图1,在△ABC中,BC=4,以线段AB为边作△ABD,使得AD=BD,连接DC,再以DC为边作△CDE,使得DC=DE,∠CDE=∠ADB=α.
(1)如图2,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;
(2)将线段CB沿着射线CE的方向平移,得到线段EF,连接BF,AF.
①若α=90°,依题意补全图3,求线段AF的长;
②请直接写出线段AF的长(用含α的式子表示).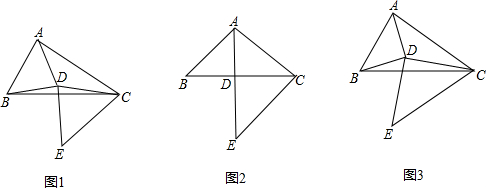
(1)如图2,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;
(2)将线段CB沿着射线CE的方向平移,得到线段EF,连接BF,AF.
①若α=90°,依题意补全图3,求线段AF的长;
②请直接写出线段AF的长(用含α的式子表示).

▼优质解答
答案和解析
(1)AD+DE=4,
理由是:如图1,
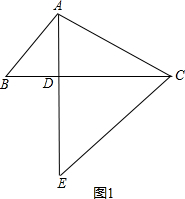
∵∠ADB=∠EDC=∠α=90°,AD=BD,DC=DE,
∴AD+DE=BC=4;
(2)①补全图形,如图2,
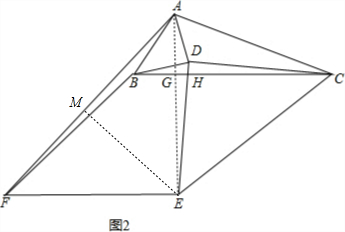
设DE与BC相交于点H,连接AE,
交BC于点G,
∵∠ADB=∠CDE=90°,
∴∠ADE=∠BDC,
在△ADE与△BDC中,
,
∴△ADE≌△BDC,
∴AE=BC,∠AED=∠BCD.
∵DE与BC相交于点H,
∴∠GHE=∠DHC,
∴∠EGH=∠EDC=90°,
∵线段CB沿着射线CE的方向平移,得到线段EF,
∴EF=CB=4,EF∥CB,
∴AE=EF,
∵CB∥EF,
∴∠AEF=∠EGH=90°,
∵AE=EF,∠AEF=90°,
∴∠AFE=45°,
∴AF=
=4
;
②如图2,过E作EM⊥AF于M,
∵由①知:AE=EF=BC,
∴∠AEM=∠FEM=
,AM=FM,
∴AF=2FM=EF×sin
=8sin
.
理由是:如图1,

∵∠ADB=∠EDC=∠α=90°,AD=BD,DC=DE,
∴AD+DE=BC=4;
(2)①补全图形,如图2,

设DE与BC相交于点H,连接AE,
交BC于点G,
∵∠ADB=∠CDE=90°,
∴∠ADE=∠BDC,
在△ADE与△BDC中,
|
∴△ADE≌△BDC,
∴AE=BC,∠AED=∠BCD.
∵DE与BC相交于点H,
∴∠GHE=∠DHC,
∴∠EGH=∠EDC=90°,
∵线段CB沿着射线CE的方向平移,得到线段EF,
∴EF=CB=4,EF∥CB,
∴AE=EF,
∵CB∥EF,
∴∠AEF=∠EGH=90°,
∵AE=EF,∠AEF=90°,
∴∠AFE=45°,
∴AF=
| EF |
| cos45° |
| 2 |
②如图2,过E作EM⊥AF于M,
∵由①知:AE=EF=BC,
∴∠AEM=∠FEM=
| α |
| 2 |
∴AF=2FM=EF×sin
| α |
| 2 |
| α |
| 2 |
看了 如图1,在△ABC中,BC=...的网友还看了以下:
英语翻译你不用担心明天,明天将会是个不同的日子.就算你遇到事情不开心,身边还有我陪着你.我会永远守候 2020-03-30 …
在矩形纸片ABCD中,按如下图所示折叠,EF为折痕,点B与点P(点P在DC边上)重合当BC与CP重 2020-04-09 …
如图,在一个直角三角形的内部做一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上(1) 2020-05-15 …
如图,在一个直角三角形的内部做一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上(1) 2020-05-15 …
如图 在平行四边形ABCD中 AE垂直于BC AF垂直于CD 垂足分别为EF (1)AB,BC,如 2020-05-15 …
如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F. P是AD的中点 2020-05-16 …
已知△ABC中,边BC的长与BC边上的高的和为20.(1)写出△ABC的面积y与BC的长x之间的函 2020-06-17 …
如图,等边三角形ABC的边长为4,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方 2020-07-12 …
已知△ABC中,边BC的长与BC边上的高的和为20.(1)写出△ABC的面积y与BC的长x之间的函 2020-07-13 …
(1)当t为何值时,四边形PQDC的面积是梯形ABCD的面积的一半(2)四边形PQDC能为平行四边 2020-07-30 …