早教吧作业答案频道 -->数学-->
在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)写出CG与EG的数量关系,并说明理由.(2)若AD=12,AB=20,求CE的长.
题目详情
在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
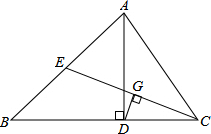
(1)写出CG与EG的数量关系,并说明理由.
(2)若AD=12,AB=20,求CE的长.

(1)写出CG与EG的数量关系,并说明理由.
(2)若AD=12,AB=20,求CE的长.
▼优质解答
答案和解析
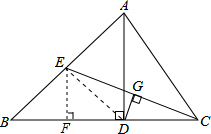 (1)CG=EG,
(1)CG=EG,
理由:连接ED,∵AD⊥BC
∴∠ADB=90°
∵CE是AB边上的中线
∴E是AB的中点
∴DE=
AB(直角三角形斜边上的中线等于斜边的一半)
又∵AE=
AB
∴AE=DE
∵AE=CD
∴DE=CD
即△DCE是等腰三角形,
∵DG⊥EC,
∴CG=EG;
(2)过点E作EF⊥BC于点F,
∵AD⊥BC,E为AB的中点,
∴EF
AD,
∴EF=6,
∵∠ADB=90°,AD=12,AB=20,
∴BD=16,
∴FD=BF=8,
∴ED=
=10,
∴DC=10,
∴EC=
=
=6
.
 (1)CG=EG,
(1)CG=EG,理由:连接ED,∵AD⊥BC
∴∠ADB=90°
∵CE是AB边上的中线
∴E是AB的中点
∴DE=
| 1 |
| 2 |
又∵AE=
| 1 |
| 2 |
∴AE=DE
∵AE=CD
∴DE=CD
即△DCE是等腰三角形,
∵DG⊥EC,
∴CG=EG;
(2)过点E作EF⊥BC于点F,
∵AD⊥BC,E为AB的中点,
∴EF
| ∥ |
. |
| 1 |
| 2 |
∴EF=6,
∵∠ADB=90°,AD=12,AB=20,
∴BD=16,
∴FD=BF=8,
∴ED=
| 62+82 |
∴DC=10,
∴EC=
| EF2+FC2 |
| 62+(8+10)2 |
| 10 |
看了 在△ABC中,AD是BC边上...的网友还看了以下:
2010年江苏省学业水平测试第33题:下图为某生态系统能量流动的部分示意图,其中数字为能量值,单位是 2020-03-30 …
把一块含45°的直角三角板ODE放在如图所示的直角坐标系中,已知动点P在斜边OD上运动,点A的坐标 2020-04-06 …
如果椭圆x2a2+y2b2=1(a>b>0)上存在点P,使P到原点的距离等于该椭圆的焦距,则椭圆的 2020-05-15 …
如图为某生态系统能量流动的部分示意图,其中数字为能量值,单位是kJ/(m2•a)能量在第二营养级和 2020-06-13 …
若变量x和y满足条件x+y−3≥0x−2y≥0,则yx的取值范围是()A.(0,12]B.(−∞, 2020-07-12 …
已知函数f(x)=sin(ωx+π3)(ω>0)在(0,2]上恰有一个最大值点和一个最小值点,则ω的 2020-11-10 …
某地区人口的出生率是1.20%,死亡率是1.08%,则该地区的人口自然增长率是[]A.1.20%B. 2020-11-11 …
(2014•达州)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点 2020-11-12 …
下图是我国某地区四项指标占全国比重的统计图。读图,完成11~12题。11.图中信息说明该区()A.水 2020-12-20 …
中心广场在钟楼的北偏东42.2°方向,那么钟楼在中心广场的()A.北偏东42°12′B.南偏西42° 2021-01-02 …