早教吧作业答案频道 -->数学-->
如图,在Rt△ABC和Rt△ABD中,∠C=∠BAD=90°,BD、AC交于点F,且AF=AD,作DE⊥AC于点E.(1)求证:∠CBF=∠ABF;(2)若AB-BC=4,AC=8,求BC的长;(3)求证:AE=CF.
题目详情
如图,在Rt△ABC和Rt△ABD中,∠C=∠BAD=90°,BD、AC交于点F,且AF=AD,作DE⊥AC于点E.
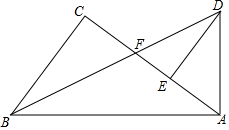
(1)求证:∠CBF=∠ABF;
(2)若AB-BC=4,AC=8,求BC的长;
(3)求证:AE=CF.

(1)求证:∠CBF=∠ABF;
(2)若AB-BC=4,AC=8,求BC的长;
(3)求证:AE=CF.
▼优质解答
答案和解析
(1)证明:∵AF=AD,
∴∠ADF=∠AFD,
∵∠AFD=∠BFC,
∴∠ADF=∠BFC,
在Rt△CBF和Rt△ABD中,
∴Rt△CBF~Rt△ABD,
∴∠CBF=∠ABF.
(2) 设BC=x,
∵AB-BC=4,
∴AB=x+4,
在Rt△ABC中,
∵AC=8,
∴(x+4)2-x2=64,
整理,可得
8x+16=64,
解得x=6,
∴BC的长是6.
(3)证明:如图1,作FG⊥AB于点G,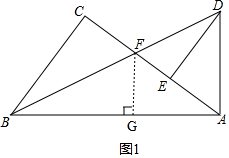 ,
,
∵∠CBF=∠ABF,
∴FG=CF,
∵∠FAG+∠DAE=90°,∠ADE+∠DAE=90°,
∴∠FAG=∠ADE,
∵∠AFG=90°-∠FAG,∠DAE=90°-∠ADE,
∴∠AFG=∠DAE,
在Rt△AFG和Rt△DAE中,
∴Rt△AFG≌Rt△DAE,
∴AE=FG,
∵FG=CF,
∴AE=CF.
∴∠ADF=∠AFD,
∵∠AFD=∠BFC,
∴∠ADF=∠BFC,
在Rt△CBF和Rt△ABD中,
|
∴Rt△CBF~Rt△ABD,
∴∠CBF=∠ABF.
(2) 设BC=x,
∵AB-BC=4,
∴AB=x+4,
在Rt△ABC中,
∵AC=8,
∴(x+4)2-x2=64,
整理,可得
8x+16=64,
解得x=6,
∴BC的长是6.
(3)证明:如图1,作FG⊥AB于点G,
 ,
,∵∠CBF=∠ABF,
∴FG=CF,
∵∠FAG+∠DAE=90°,∠ADE+∠DAE=90°,
∴∠FAG=∠ADE,
∵∠AFG=90°-∠FAG,∠DAE=90°-∠ADE,
∴∠AFG=∠DAE,
在Rt△AFG和Rt△DAE中,
|
∴Rt△AFG≌Rt△DAE,
∴AE=FG,
∵FG=CF,
∴AE=CF.
看了 如图,在Rt△ABC和Rt△...的网友还看了以下:
设A是数集,且满足条件:若a∈A,a≠1则1—a分之1∈A(2)集合A有没有可能为单元素集合?(3 2020-04-05 …
设A为实数集且满足条件:若a∈A,则1/(1-a)∈A(a不等于1)怎么证明A不可能是单元素集还有 2020-04-05 …
设n阶方阵A满足A^3=0,则下列矩阵 B=A-E,C=A+E,D=A^2-A,F=A^2+A中可 2020-04-05 …
已知a,b,c是不全相等的整数,求证2(a^3+b^3+c^3)>(a^2)(b+c)+(b^2) 2020-04-22 …
已知a,b,c均为正整数,且满足a的平方,b的平方,c的平方,有a为质数,求证2(a+b+1)是完 2020-05-17 …
已知a+b+c=1,求证:√2≤√(a^2+b^2)+√(b^2+c^2)+√(c^2+a^2)≤ 2020-05-20 …
把有理数分成以下两类A={a│a∈Q,a≤0或a>0但a20且b2>2}这是有理数系的一个分划,我 2020-06-12 …
为验证“酸的化学通性”,某班同学在实验室进行如下实验.请分析并回答相关问题:(1)写出能证明A中反 2020-07-24 …
为验证“酸的化学通性”,某班同学在实验室进行如下实验.请分析并回答相关问题:(1)写出能证明A中反 2020-07-29 …
设数集A满足:若x∈A(x≠1,x≠0),则11-x∈A(1)若2∈A,试证明A中还有另外两个元素 2020-07-30 …