早教吧作业答案频道 -->数学-->
如图,△ABC中,∠C=90°,AC=4,BC=3,正方形DEFG的四个顶点分别在边AC、AB、CB上.(1)求证:△ADE∽△GBF;(2)求正方形DEFG的边长;(3)连结CE、CF分别交DG于点P、Q.求证:PQ2=PD•QG.
题目详情
如图,△ABC中,∠C=90°,AC=4,BC=3,正方形DEFG的四个顶点分别在边AC、AB、CB上.
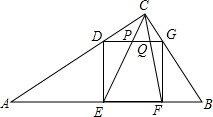
(1)求证:△ADE∽△GBF;
(2)求正方形DEFG的边长;
(3)连结CE、CF分别交DG于点P、Q.求证:PQ2=PD•QG.

(1)求证:△ADE∽△GBF;
(2)求正方形DEFG的边长;
(3)连结CE、CF分别交DG于点P、Q.求证:PQ2=PD•QG.
▼优质解答
答案和解析
证明:(1)∵直角△ADE中,∠A+∠ADE=90°,
又∵直角△ABC中,∠A+∠B=90°,
∴∠ADE=∠B,
又∵∠AED=∠GFB,
∴△ADE∽△GBF;
(2)在直角△ABC中,AB=
=
=5,
则AB边上的高是:
=2.4,
∵DG∥AB,
∴△CDG∽△CAB,
∴设正方形DEFG的边长是x,则
=
,
解得:x=
;
(3)∵△ADE∽△GBF,
∴
=
,则DE•GF=AE•BF,
又∵EF=DE=GF,
∴EF2=AE•BF,
∵DP∥AE,
∴△CDP∽△CAE,
∴
=
,
同理,
=
=
,
则
=
=
,
∴
=
,
∴PQ2=PD•QG.
又∵直角△ABC中,∠A+∠B=90°,
∴∠ADE=∠B,
又∵∠AED=∠GFB,
∴△ADE∽△GBF;
(2)在直角△ABC中,AB=
| AC2+BC2 |
| 32+42 |
则AB边上的高是:
| 3×4 |
| 5 |
∵DG∥AB,
∴△CDG∽△CAB,
∴设正方形DEFG的边长是x,则
| x |
| 5 |
| 2.4-x |
| 2.4 |
解得:x=
| 60 |
| 37 |
(3)∵△ADE∽△GBF,
∴
| DE |
| AE |
| BF |
| GF |
又∵EF=DE=GF,
∴EF2=AE•BF,
∵DP∥AE,
∴△CDP∽△CAE,
∴
| CD |
| AC |
| DP |
| AE |
同理,
| CD |
| AC |
| PQ |
| EF |
| QG |
| BF |
则
| DP |
| AE |
| QG |
| BF |
| PQ |
| EF |
∴
| DP•DQ |
| AE•BF |
| PQ•EF |
| EF2 |
∴PQ2=PD•QG.
看了 如图,△ABC中,∠C=90...的网友还看了以下:
已知函数f(x)=sin(x-π/6)+cos(x-π/3).g(x)=2sin平方x/2.(1) 2020-05-16 …
如何判断浮力公式的使用浮力公式一共大概五个:1.F浮=G物2.F浮=F向上—F向下3.F浮=G-F 2020-05-16 …
已知f(x)=5x/x+3,f[g(x)]=4-x已知函数f(x)=5x/x+3,f[g(x)]= 2020-05-17 …
已知函数fx=...Fx=a√1-x^2+√1+x+√1-x的最大值为g(a)1)设t=√1+x+ 2020-06-08 …
如何用matlab解方程组?这个八个未知数的方程组是不是用matlab解不出来?[a,b,c,d, 2020-07-09 …
正整数可以分为两个互不相交的正整数子集:{f(1),f(2),f(3)...f(n)...};{g 2020-07-20 …
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-2,2].( 2020-07-20 …
若函数f(x)的定义域为(-3,5),求g(x)=f(-x)+f(2x+5)的定义域 2020-07-25 …
一个关于牛顿第三定律问题一吊扇重力G,用一铁杆使之与天花板相连,当吊扇转动时,杆对吊扇拉力为F,求G 2020-11-21 …
已知函数F=(x)=x+1/x-1,(1)求F(x)的定义域和值域已知函数F=(x)=x+1/x-1 2021-01-31 …