设函数f（x）=x3-3x2-ax+5-a，若存在唯一的正整数x0，使得f（x0）<0，则a的取值范围是（）A.（0，13）B.（13，54]C.（13，32]D.（54，32]

Question

设函数f（x）=x³-3x²-ax+5-a，若存在唯一的正整数x₀，使得f（x₀）<0，则a的取值范围是（　　）

A. （0，

(1)/(3)）

B. （

(1)/(3)，(5)/(4)]

C. （

(1)/(3)，(3)/(2)]

D. （

(5)/(4)，(3)/(2)]

Answer 1

设g（x）=x³-3x²+5，h（x）=a（x+1），
两个函数图象如图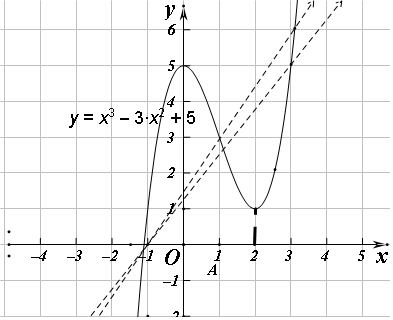：要使存在唯一的正整数x₀，
使得f（x₀）<0，只要

g(1)≥h(1)

g(3)<h(3)

，即

1-3+5≥2a

27-27+5<4a

，
解得(5)/(4)<a≤(3)/(2)；
故选D．