早教吧作业答案频道 -->数学-->
如图,AB⊥MN于A,CD⊥MN于D.点P是MN上一个动点.(1)如图①.BP平分∠ABC,CP平分∠BCD交BP于点P.若AB=4,CD=6.试求AD的长;(2)如图②,∠BPC=∠BPA,BC⊥BP,若AB=4,求CD的长.
题目详情
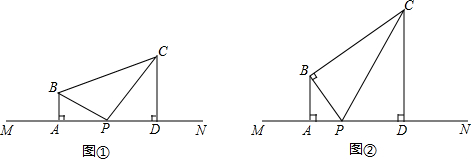
如图,AB⊥MN于A,CD⊥MN于D.点P是MN上一个动点.
(1)如图①.BP平分∠ABC,CP平分∠BCD交BP于点P.若AB=4,CD=6.试求AD的长;
(2)如图②,∠BPC=∠BPA,BC⊥BP,若AB=4,求CD的长.
(1)如图①.BP平分∠ABC,CP平分∠BCD交BP于点P.若AB=4,CD=6.试求AD的长;
(2)如图②,∠BPC=∠BPA,BC⊥BP,若AB=4,求CD的长.

▼优质解答
答案和解析
(1)过点P作PE⊥BC于E,过点B作BF⊥CD于F,
∵AB⊥MN于A,CD⊥MN于D,BP平分∠ABC,
∴AP=PE,
在Rt△ABP和Rt△EBP中,
,
∴Rt△ABP≌Rt△EBP,
∴AB=BE=4,
同理可得CE=CD=6,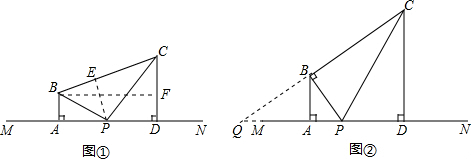
∴BC=BE+CE=10,
易证四边形ABFD是矩形,
∴BF=AD,CF=6-4=2,
∴AD=
=4
;
(2)延长CB和PA,记交点为点Q.
∵∠BPC=∠BPA,BC⊥BP,
∴QB=BC(等腰三角形“三合一”的性质).
∵BA⊥MN,CD⊥MN,
∴AB∥CD,
∴△QAB∽△QDC,
∴
=
=
,
∴CD=2AB=2×4=8.
∵AB⊥MN于A,CD⊥MN于D,BP平分∠ABC,
∴AP=PE,
在Rt△ABP和Rt△EBP中,
|
∴Rt△ABP≌Rt△EBP,
∴AB=BE=4,
同理可得CE=CD=6,

∴BC=BE+CE=10,
易证四边形ABFD是矩形,
∴BF=AD,CF=6-4=2,
∴AD=
| BC2-CF2 |
| 6 |
(2)延长CB和PA,记交点为点Q.
∵∠BPC=∠BPA,BC⊥BP,
∴QB=BC(等腰三角形“三合一”的性质).
∵BA⊥MN,CD⊥MN,
∴AB∥CD,
∴△QAB∽△QDC,
∴
| AB |
| CD |
| QB |
| QC |
| 1 |
| 2 |
∴CD=2AB=2×4=8.
看了 如图,AB⊥MN于A,CD⊥...的网友还看了以下:
A2+B2═2AB的反应历程可以看作如下(△H表示该过程的能量变化):Ⅰ.A2═A+A△H1Ⅱ.B 2020-04-11 …
设A、B、C为三角形的三内角,且方程(sinB-sinA)x2+(sinA-sinC)x +(si 2020-05-16 …
相似矩阵充分条件(见一道选择题)如果,则n阶矩阵A与矩阵B相似.A./A/=/B/B.r(A)=r 2020-05-21 …
设3/7用小数来表示时其小数点后第2010个数字为a,且|b|=b+2010,则|2b+10a|- 2020-06-11 …
(2008•广东)如图为甲病(A-a)和乙病(B-b)的遗传系谱图,其中乙病为伴性遗传病,请回答下 2020-06-18 …
23.中国画中,常用梅、兰、竹、菊来表示人格,这种方式涉及的意象类型是.A.仿象B.兴象C.喻象1 2020-06-20 …
设A、B是非空数集,定义:A⊕B={a+b|a∈A,b∈B},若A={1,2,3},B={4,5, 2020-07-01 …
根据有理数的运算律,下列运算正确的是()A.a-b=b-aB.m(a-b+c)=ma-mb+mcC 2020-07-31 …
本题为选做题.包括A、B两题.选学《化学与生活》模块的考生答A题.选学《有机化学基础》模块的考生答B 2020-12-18 …
c若有变量说明:inta=0,b=0,c=0;,以下符合C语言语法的赋值表达式是:A.a=9+b+c 2020-12-31 …