早教吧作业答案频道 -->数学-->
已知椭圆C:x24+y22=1的焦点分别为F1,F2.(Ⅰ)求以线段F1,F2为直径的圆的方程;(Ⅱ)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?
题目详情
已知椭圆C:
+
=1的焦点分别为F1,F2.
(Ⅰ)求以线段F1,F2为直径的圆的方程;
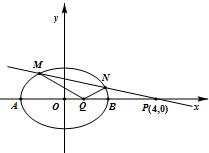
(Ⅱ)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明理由.
| x2 |
| 4 |
| y2 |
| 2 |
(Ⅰ)求以线段F1,F2为直径的圆的方程;
(Ⅱ)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(本小题满分13分)
( I)因为a2=4,b2=2,所以c2=2.
所以以线段F1F2为直径的圆的方程为x2+y2=2.…(3分)
( II)若存在点Q(m,0),使得∠PQM+∠PQN=180°,
则直线QM和QN的斜率存在,分别设为k1,k2.
等价于k1+k2=0.
依题意,直线l的斜率存在,故设直线l的方程为y=k(x-4).
由
,得(2k2+1)x2-16k2x+32k2-4=0.
因为直线l与椭圆C有两个交点,所以△>0.
即(16k2)2-4(2k2+1)(32k2-4)>0,解得k2<
.
设M(x1,y1),N(x2,y2),则x1+x2=
,x1x2=
,y1=k(x1-4),y2=k(x2-4).
令k1+k2=
+
=0,(x1-m)y2+(x2-m)y1=0,(x1-m)k(x2-4)+(x2-m)k(x1-4)=0,
当k≠0时,2x1x2-(m+4)(x1+x2)+8m=0,
所以2×
-(m+4)×
+8m=0,
化简得,
=0,
所以m=1.
当k=0时,也成立.
所以存在点Q(1,0),使得∠PQM+∠PQN=180°.…(14分)
( I)因为a2=4,b2=2,所以c2=2.
所以以线段F1F2为直径的圆的方程为x2+y2=2.…(3分)
( II)若存在点Q(m,0),使得∠PQM+∠PQN=180°,
则直线QM和QN的斜率存在,分别设为k1,k2.
等价于k1+k2=0.
依题意,直线l的斜率存在,故设直线l的方程为y=k(x-4).
由
|
因为直线l与椭圆C有两个交点,所以△>0.
即(16k2)2-4(2k2+1)(32k2-4)>0,解得k2<
| 1 |
| 6 |
设M(x1,y1),N(x2,y2),则x1+x2=
| 16k2 |
| 2k2+1 |
| 32k2-4 |
| 2k2+1 |

令k1+k2=
| y1 |
| x1-m |
| y2 |
| x2-m |
当k≠0时,2x1x2-(m+4)(x1+x2)+8m=0,
所以2×
| 32k2-4 |
| 2k2+1 |
| 16k2 |
| 2k2+1 |
化简得,
| 8(m-1) |
| 2k2+1 |
所以m=1.
当k=0时,也成立.
所以存在点Q(1,0),使得∠PQM+∠PQN=180°.…(14分)
看了 已知椭圆C:x24+y22=...的网友还看了以下:
椭圆.求与椭圆x^2+(y^2/81)=1有相同焦点,且经过P(3,-3)的椭圆方程(步骤详细点) 2020-05-15 …
高中数学空间椭圆综合题设两个半径为1的大球面外切,且都与半径1的圆柱面内切,另一个小球面与这两个大 2020-05-16 …
高中椭圆,求解 1,若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,焦距为6,则椭圆方程为? 2 2020-05-16 …
椭圆求圆心已知一个椭圆方程,求圆心坐标.(x-x0)^2/a^2+(y-y0)^2/b^2=1已知 2020-05-21 …
椭圆求证问题已知椭圆x²/a²+y²/b²=1短轴的两端点为点A、点B.(a>b>0)P为椭圆上不 2020-07-07 …
一个椭圆能否由4个等圆的一段圆弧组成,能的话解答下面的题目,不能的话直接把这问题拍死!椭圆的长半轴 2020-07-31 …
求一个椭圆周长一个长轴7米,短轴3米的椭圆,求周长注意是长轴,不是长半轴要求用积分精确地计算,不要 2020-07-31 …
设椭圆x2/a2+y2/b2=1的上下顶点分别为B1B2若点P为椭圆上的一点且直线PB1PB2的斜 2020-08-01 …
椭圆求标准方程!设椭圆的中心在原点,坐标为对称轴,一个焦点与短轴的连线互相垂直,且此焦点与长轴上较 2020-08-02 …
一椭圆求面积最大值问题已知椭圆c:x^/a^+y^/b^=1(a>b>0)的离心率为√6/3,短轴的 2020-11-04 …