如图，已知点A（5，0），B（0，5），把一个直角三角尺DEF放在△OAB内，使其斜边FD在线段AB上，三角尺可沿着线段AB上下滑动，其中∠EFD=45°，ED=2，点G为边FD的中点．（1）求直线AB的解析式；

Question

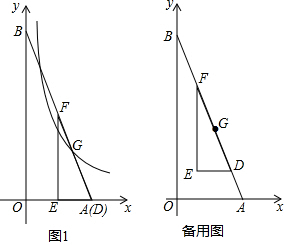
如图，已知点A（5，0），B（0，5），把一个直角三角尺DEF放在△OAB内，使其斜边FD在线段AB上，三角尺可沿着线段AB上下滑动，其中∠EFD=45°，ED=2，点G为边FD的中点．
（1）求直线AB的解析式；
（2）如图1，当点D与点A重合时，求经过点G的反比例函数y=(k)/(x)（k≠0）的解析式；
（3）在三角尺滑动的过程中，经过点G的反比例函数的图象能否同时经过点F？如果能，求出此时反比例函数的解析式，如果不能，说明理由．

Answer 1

（1）设直线AB的解析式为y=ax+b，
把A、B坐标代入可得

5a+b=0

b=5

，解得

a=-1

b=5

，
∴直线AB的解析式为y=-x+5；
（2）∵A（5，0），
∴OA=5，
当D与A重合时，则OE=OD-DE=5-2=3，
∵∠EFD=45°，
∴EF=DE=2，
∵F（3，2），D（5，0），
∵G为DF的中点，
∴G（4，1），
∴k=4×1=4，
∴经过点G的反比例函数的解析式为y=(4)/(x)；
（3）设F（t，-t+5），
则D点横坐标为t+2，代入直线AB解析式可得y=-（t+2）+5=-t+3，
∴D（t+2，-t+3），
∵G为DF中点，
∴G（t+1，-t+4），
若反比例函数同时过G、F点，则可得t（-t+5）=（t+1）（-t+4），
解得t=2，此时F点坐标为（2，3），
设过F、G的反比例函数解析式为y=(s)/(x)，则s=2×3=6，
∴经过点G的反比例函数的图象能同时经过点F，其函数解析式为y=(6)/(x)．