早教吧作业答案频道 -->数学-->
如图①,已知∠MON=Rt∠,点A,P分别是射线OM,ON上两定点,且OA=2,OP=6,动点B从点O向点P运动,以AB为斜边向右侧作等腰直角△ABC,设线段OB的长x,点C到射线ON的距离为y.(1)若OB=2,直接写
题目详情
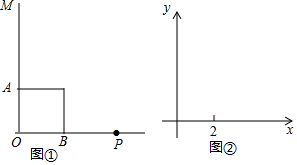
如图①,已知∠MON=Rt∠,点A,P分别是射线OM,ON上两定点,且OA=2,OP=6,动点B从点O向点P运动,以AB为斜边向右侧作等腰直角△ABC,设线段OB的长x,点C到射线ON的距离为y.
(1)若OB=2,直接写出点C到射线ON的距离;
(2)求y关于x的函数表达式,并在图②中画出函数图象;
(3)当动点B从点O运动到点P,求点C运动经过的路径长.
(1)若OB=2,直接写出点C到射线ON的距离;
(2)求y关于x的函数表达式,并在图②中画出函数图象;
(3)当动点B从点O运动到点P,求点C运动经过的路径长.

▼优质解答
答案和解析
(1)如图①中,
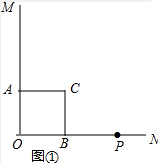
∵OA=OB=2,∠AOB=90°,△ACB是等腰直角三角形,
∴四边形OACB是正方形,
∴点C到ON的距离为2.
(2)如图③中,作CE⊥OA于E,CF⊥ON于F.
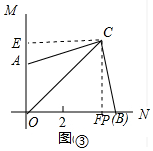
∵∠ACB=∠ECF=90°,CA=CB,∠CEA=∠CFB=90°,
∴△CEA≌△CFB,
∴AE=CF,CE=CF,
∵∠CEO=∠CFO=∠EOF=90°,
∴四边形OECF是矩形,∵CE=CF,
∴四边形OECF是正方形,
∴CF=CE=OE=OF=y,
∵AE=y-2,FB=x-y,
∴y-2=x-y,
∴y=
x+1,可得函数图象如图②所示,
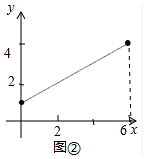
(3)如图③中,∵CE=CF,
∴OC平分∠MON,
∴点C的运动轨迹是线段OC,
∵x=6,y=4,
∴OC=4
,
∴点C运动经过的路径长为4
.

∵OA=OB=2,∠AOB=90°,△ACB是等腰直角三角形,
∴四边形OACB是正方形,
∴点C到ON的距离为2.
(2)如图③中,作CE⊥OA于E,CF⊥ON于F.

∵∠ACB=∠ECF=90°,CA=CB,∠CEA=∠CFB=90°,
∴△CEA≌△CFB,
∴AE=CF,CE=CF,
∵∠CEO=∠CFO=∠EOF=90°,
∴四边形OECF是矩形,∵CE=CF,
∴四边形OECF是正方形,
∴CF=CE=OE=OF=y,
∵AE=y-2,FB=x-y,
∴y-2=x-y,
∴y=
| 1 |
| 2 |

(3)如图③中,∵CE=CF,
∴OC平分∠MON,
∴点C的运动轨迹是线段OC,
∵x=6,y=4,
∴OC=4
| 2 |
∴点C运动经过的路径长为4
| 2 |
看了 如图①,已知∠MON=Rt∠...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
已知实数a,b满足a+b=8,ab=15,且a>b,试求a-b的值解a+b=8,ab=15(a+b 2020-05-17 …
如图正方形被一条曲线分成A、B两部分,下面()说法正确.A.如果a>b,那么A周长大于B周长B.如 2020-05-17 …
同学们植树,成活了a棵,死了b棵,成活率是()a.a/b*100%b.b/a*100%c.a同学们 2020-06-03 …
对方阵A实行初等变换得距阵B,若|A|不等于0,则A.必有|A|=|B|B.必有|A|不等于|对方 2020-06-18 …
2、已知a,b为非零向量,则下列命题中真命题的个数为A若|a|+|b|=|a+b|,则a与b方向相 2020-07-30 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
下面的等量代换怎么做1.A+B=20,B+C=12,C+A=18,ABC各多少2.A+A+A=B+ 2020-08-02 …
数学老师给学生出了一道题,计算:(2(a+b)^5-3(a+b)^4+(-a-b)^3)/(2(a+ 2020-12-09 …
数轴上点A,B所代表的数为a,b,请你计算A,B两点的距离.a=2,b=6,A,B的距离是什么;a- 2020-12-30 …