早教吧作业答案频道 -->数学-->
如图,O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.(1)如图1,当∠ACD=45°时,求证:DE是O的切线;(2)如图2,当点F是CD的
题目详情
如图, O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是 O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.
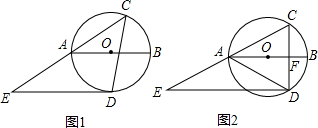
(1)如图1,当∠ACD=45°时,求证:DE是 O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

▼优质解答
答案和解析
(1)证明:如图1中,连接OD.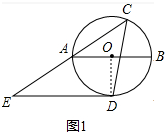
∵∠C=45°,
∴∠AOD=2∠C=90°,
∵ED∥AB,
∴∠AOD+∠EDO=180°,
∴∠EDO=90°,
∴ED⊥OD,
∴ED是 O切线.
(2) 如图2中,连接BC,
∵CF=DF,
∴AF⊥CD,
∴AC=AD,
∴∠ACD=∠ADC,
∵AB∥ED,
∴ED⊥DC,
∴∠EDC=90°,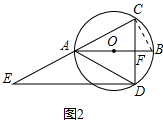
在RT△ACB中,∵∠ACB=90°,∠CAB=30°,AB=2,
∴BC=1,AC=
,
∴CF=
AC=
,CD=2CF=
,
在RT△ECD中,
∵∠EDC=90°,CD=
,∠E=∠CAB=30°,
∴EC=2CD=2
,ED=
=3,
∴S△ECD=
•ED•CD=
.

∵∠C=45°,
∴∠AOD=2∠C=90°,
∵ED∥AB,
∴∠AOD+∠EDO=180°,
∴∠EDO=90°,
∴ED⊥OD,
∴ED是 O切线.
(2) 如图2中,连接BC,
∵CF=DF,
∴AF⊥CD,
∴AC=AD,
∴∠ACD=∠ADC,
∵AB∥ED,
∴ED⊥DC,
∴∠EDC=90°,

在RT△ACB中,∵∠ACB=90°,∠CAB=30°,AB=2,
∴BC=1,AC=
| 3 |
∴CF=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
在RT△ECD中,
∵∠EDC=90°,CD=
| 3 |
∴EC=2CD=2
| 3 |
| EC2-CD2 |
∴S△ECD=
| 1 |
| 2 |
3
| ||
| 2 |
看了 如图,O的直径AB的长为2,...的网友还看了以下:
A、B、W、D、E为短周期元素,且原子序数依次增大,质子数之和为40,B、W同周期,D、E同周期, 2020-04-08 …
A、B、C、D、E是五种短周期元素,F是过渡元素.A、B、C、E同周期,C、D同主族,A元素在地壳 2020-04-13 …
在“所有的大学生是学生”和“有的学生是大学”这两个判断中,谓项都是()A.都是周延的B.都是不周延 2020-05-13 …
逻辑学指出下题包含何种推理?请指出推理形式.全称肯定判断的谓项不周延,特称肯定判断的谓项不周延,所 2020-06-29 …
血液中CO2浓度对呼吸的调节主要是通过()A.刺激延髓腹外侧浅表部位B.直接刺激呼吸中枢C.肺牵张 2020-07-01 …
如图,P是菱形ABC尸对角线BD上一点,连接CP并延长,交AD于E,交BA延长线于F.(1)求证如 2020-07-16 …
(2000•海淀区)已知:如图,四边形ABCD是⊙O的内接四边形,A是弧BD的中点,过A点的切线与 2020-07-20 …
您好!三段论第四格PAMMASSIP大前提中的大项P在前提中是周延的,但到了结论中却是不周延的,三段 2020-12-02 …
A、B、C、D、E五种短周期元素,原子序数E>D>A>B>C,且A、B、D、E同周期,A、C同主族, 2020-12-05 …
“凡贪污罪都是故意犯罪;该行为是故意犯罪,所以,该行为是贪污罪。”这个三段论所犯的逻辑错误是A、大项 2020-12-06 …