早教吧作业答案频道 -->数学-->
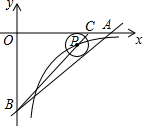
如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,P的圆心P在线段BC上,且P与边AB,AO都相切.若反比例函数y=kx(k≠0)的图象经过圆心P,则k=.
题目详情
如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2, P的圆心P在线段BC上,且 P与边AB,AO都相切.若反比例函数y=
(k≠0)的图象经过圆心P,则k=___.
| k |
| x |

▼优质解答
答案和解析
作PD⊥OA于D,PE⊥AB于E,作CH⊥AB于H,如图,设 P的半径为r,
∵ P与边AB,AO都相切,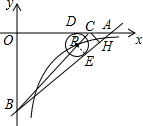
∴PD=PE=r,AD=AE,
在Rt△OAB中,∵OA=8,AB=10,
∴OB=
=6,
∵AC=2,
∴OC=6,
∴△OBC为等腰直角三角形,
∴△PCD为等腰直角三角形,
∴PD=CD=r,
∴AE=AD=2+r,
∵∠CAH=∠BAO,
∴△ACH∽△ABO,
∴
=
,即
=
,解得CH=
,
∴AH=
=
=
,
∴BH=10-
=
,
∵PE∥CH,
∴△BEP∽△BHC,
∴
=
,即
=
,解得r=1,
∴OD=OC-CD=6-1=5,
∴P(5,-1),
∴k=5×(-1)=-5.
故答案为-5.
∵ P与边AB,AO都相切,

∴PD=PE=r,AD=AE,
在Rt△OAB中,∵OA=8,AB=10,
∴OB=
| 102-82 |
∵AC=2,
∴OC=6,
∴△OBC为等腰直角三角形,
∴△PCD为等腰直角三角形,
∴PD=CD=r,
∴AE=AD=2+r,
∵∠CAH=∠BAO,
∴△ACH∽△ABO,
∴
| CH |
| OB |
| AC |
| AB |
| CH |
| 6 |
| 2 |
| 10 |
| 6 |
| 5 |
∴AH=
| AC2-CH2 |
22-(
|
| 8 |
| 5 |
∴BH=10-
| 8 |
| 5 |
| 42 |
| 5 |
∵PE∥CH,
∴△BEP∽△BHC,
∴
| BE |
| BH |
| PE |
| CH |
| 10-(2+r) | ||
|
| r | ||
|
∴OD=OC-CD=6-1=5,
∴P(5,-1),
∴k=5×(-1)=-5.
故答案为-5.
看了 如图,OA在x轴上,OB在y...的网友还看了以下:
边缘粗糙,半径不同的两个轮子,作无滑动的摩擦传动.AB是大轮O上的两点,OA=R=0.8m,OB= 2020-05-13 …
有联接点O(0,0)和点A(1,1)一段向上凸的曲线弧OA,对于OA上任一点P(x,y)曲线OP与 2020-05-17 …
在平面直角坐标系中,矩形OABC,O(0,0),A(2,0),C(0,1),将矩形折叠,使O点落在 2020-05-20 …
在坐标平面上有一质点从O(0,0)出发,逐步移动,每一步的长度均为1,每一步等可能的向上向下向左向 2020-07-20 …
设有联接点O(0,0)和点A(1,1)一段向上凸的曲线弧OA,对于OA上任一点P(x,y)………… 2020-07-26 …
⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是()A. 2020-07-26 …
已知xyz三维坐标系上点A(0,0,1),B(1,1,0),C(0,1,0),O(0,0,0),已 2020-07-30 …
已知三角形AOC,点O(0,0),点C(4,0),点A在直线y=-x+3的图像上已知三角形AOC, 2020-07-30 …
如图,△OAB的三个顶点坐标分别为O(0,0),A(5,O)B(2,4).(1)求△ABO的面积,( 2020-11-04 …
已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8, 2020-12-25 …