早教吧作业答案频道 -->数学-->
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;(2)若点P在线段AB上.①如图2,连
题目详情
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
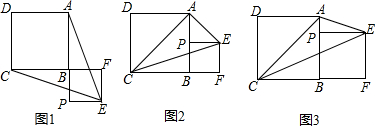
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
▼优质解答
答案和解析
(1)∵四边形ABCD和四边形BPEF是正方形,
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
,
∴△APE≌△CFE,
∴EA=EC;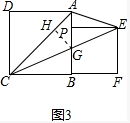
(2)①∵P为AB的中点,
∴PA=PB,又PB=PE,
∴PA=PE,
∴∠PAE=45°,又∠DAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
②∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a
∵PE∥CF,
∴
=
,即
=
,
解得,a=
b;
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=
AG=
×(2
b-2b)=(2-
)b,又BG=2b-a=(2-
)b,
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴a:b=
:1;∴∠AEC=45°.
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
|
∴△APE≌△CFE,
∴EA=EC;

(2)①∵P为AB的中点,
∴PA=PB,又PB=PE,
∴PA=PE,
∴∠PAE=45°,又∠DAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
②∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a
∵PE∥CF,
∴
| PE |
| BC |
| PG |
| GB |
| b |
| a |
| a-b |
| 2b-a |
解得,a=
| 2 |
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴a:b=
| 2 |
看了 已知正方形ABCD,P为射线...的网友还看了以下:
完成下列实验所选择的装置或仪器正确的是()A.构成锌铜原电池B.测定酸碱中和反应中和热大小的量热计 2020-05-14 …
已知A=w-x+y-z,我们约定“将w换成x,同时将Z换成y,y换成z,z换成w”算是作了一次“轮 2020-06-12 …
下列简单实验方案,不能实现实验目的是()A.①验证硫酸、碳酸、硅酸酸性强弱B.②检验溴乙烷发生消去 2020-07-29 …
补全证明过程:已知:如图,∠1=∠2,∠C=∠D.求证:∠A=∠F.证明:∵∠1=∠2(已知),又 2020-08-02 …
如图,已知:AF、BD、CE、ABC、DEF均是直线,∠EQF=∠APB,∠C=∠D.求证:∠A= 2020-08-02 …
证明反比性质和更比性质1.如果a/b=c/d,求证b/a=d/c.2.如果a/b=c/d,求证a/c 2020-10-30 …
一、能证明的证明,不能的举反例哦!1、如果a>b,判断a-c与b-c的大小2、如果a>b,cb,c> 2020-11-27 …
在已出土的商代青铜器中,相当多的是酒器。由此可以[]A.推断商代的农业生产比较发达B.印证文献记载商 2020-12-07 …
补全证明过程已知:如图,∠1=∠2,∠C=∠D.求证:∠A=∠F.证明:∵∠1=∠2(已知),又∵∠ 2021-01-07 …
格里菲思用肺炎双球菌在小鼠身上进行了著名的转化实验,此实验结果()A.证明了DNA是遗传物质B.证明 2021-01-08 …