早教吧作业答案频道 -->数学-->
如图①,在△ABC中,∠A=50°,有一块直角三角尺PMN放置在△ABC上(点P在△ABC内),使三角尺PMN的两条直角边PM、PN恰好分别经过点B、C.(1)填空:∠ABC+∠ACB=,∠PBC+∠PCB=;(2)试问
题目详情
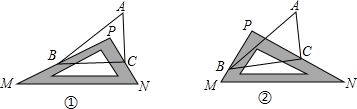
如图①,在△ABC中,∠A=50°,有一块直角三角尺PMN放置在△ABC上(点P在△ABC内),使三角尺PMN的两条直角边PM、PN恰好分别经过点B、C.
(1)填空:∠ABC+∠ACB=___,∠PBC+∠PCB=___;
(2)试问∠ABP与∠ACP是否存在某种确定的数量关系,请写出你的结论;
(3)如图②,改变直角三角尺PMN的位置(点P在△ABC外),三角尺PMN的两条直角边PM、PN仍然分别经过点B、C,(2)中的结论是否仍然成立?若不成立,请写出你的结论,并说明理由.
(1)填空:∠ABC+∠ACB=___,∠PBC+∠PCB=___;
(2)试问∠ABP与∠ACP是否存在某种确定的数量关系,请写出你的结论;
(3)如图②,改变直角三角尺PMN的位置(点P在△ABC外),三角尺PMN的两条直角边PM、PN仍然分别经过点B、C,(2)中的结论是否仍然成立?若不成立,请写出你的结论,并说明理由.

▼优质解答
答案和解析
(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABC+∠ACB=130°;∠PBC+∠PCB=90°.
(2)∠ABP+∠ACP=40°.
∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP+∠ACP
=(∠ABC-∠PBC)+(∠ACB-∠PCB)
=(∠ABC+∠ACB)-(∠PBC+∠PCB)
=130°-90°
=40°.
(3)发生变化.
∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,(三角形内角和180°)
∵∠MPN=90°,
∴∠PBC+∠PCB=90°,(三角形内角和180°)
∴∠ACP-∠ABP=130°-90°=40°.
∴∠ABC+∠ACB=180°-50°=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABC+∠ACB=130°;∠PBC+∠PCB=90°.
(2)∠ABP+∠ACP=40°.
∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP+∠ACP
=(∠ABC-∠PBC)+(∠ACB-∠PCB)
=(∠ABC+∠ACB)-(∠PBC+∠PCB)
=130°-90°
=40°.
(3)发生变化.
∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,(三角形内角和180°)
∵∠MPN=90°,
∴∠PBC+∠PCB=90°,(三角形内角和180°)
∴∠ACP-∠ABP=130°-90°=40°.
看了 如图①,在△ABC中,∠A=...的网友还看了以下:
阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1- 2020-06-14 …
数轴上两点A,B对应的书分别为-1,4,点p为数轴上一动点,其对应的数为x若点p到点a,点b的距离 2020-06-26 …
已知A,B是数轴上两点.A点表示-1,B点表示3.5,A,B两点的距离. 2020-07-12 …
数轴上两点A,B对应的数分别为-1,4,点P为数轴上一动点,其对应的数为x(1)若点P到点A,点B 2020-07-16 …
将六个人分成四组,其中两个组各二人,另外两个组各一人,派到四个不同地方服务,几种分配方法?答案中要 2020-07-21 …
附加题:已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.(1)若点 2020-07-30 …
已知数轴上两点A、B对应的数分别为a和b,且a、b满足|a+3|+|b-4|=0.(1)求a、b并 2020-07-30 …
数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a 2020-08-03 …
点A、B在数轴上表示的数分别为-12和16.(规定数轴上两点A、B之间的距离记为AB)(1)点C在 2020-08-03 …
如图所示,在平面直角坐标系中,给定y轴正半轴上两点A(0,a),B(0,b)(a>b>0).试在x轴 2021-01-16 …