早教吧作业答案频道 -->数学-->
如图1,在Rt△ABC中,∠ACB=90°,D为CB上一点,且满足CD=CA,连接AD.过点C作CE⊥AB于点E.(1)若AB=10,BD=2,求CE的长;(2)如图2,若点F是线段CE延长线上一点,连接FD,若∠F=30°,求证:CF=AE+
题目详情
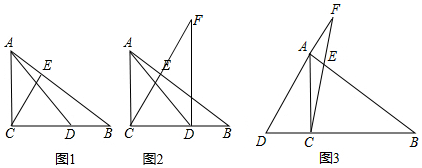
如图1,在Rt△ABC中,∠ACB=90°,D为CB上一点,且满足CD=CA,连接AD.过点C作CE⊥AB于点E.
(1)若AB=10,BD=2,求CE的长;
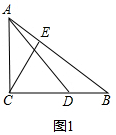
(2)如图2,若点F是线段CE延长线上一点,连接FD,若∠F=30°,求证:CF=AE+
DF;
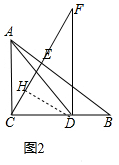
(3)如图3,设D为BC延长线上一点,其它条件不变,直线CE与直线AD交于点F,若∠F=30°,请直接写出线段CF,AE,DF之间的关系,不需要说明理由.
(1)若AB=10,BD=2,求CE的长;
(2)如图2,若点F是线段CE延长线上一点,连接FD,若∠F=30°,求证:CF=AE+
| ||
| 2 |
(3)如图3,设D为BC延长线上一点,其它条件不变,直线CE与直线AD交于点F,若∠F=30°,请直接写出线段CF,AE,DF之间的关系,不需要说明理由.

▼优质解答
答案和解析
(1) 如图1中,设AC=CD=x.
在Rt△ACB中,AB=10,AC=x,BC=CD+BD=x+2,
∵AB2=AC2+BC2,
∴102=x2+(x+2)2,
解得x=6或-8(舍弃),
∴AC=6.
∵
•AC•BC=
•AB•CE,
∴CE=
=
.
(2)证明:如图2中,作DH⊥CF于H.
∵∠ACD=∠AEC=∠DHC=90°,
∴∠ACE+∠CAE=90°,∵∠ACE+∠BCE=90°,
∴∠CAE=∠DCH,
在△ACE和∠CDH中,
,
∴△ACE≌△CDH,
∴AE=CH,
在Rt△DHF中,∵∠DHF=90°,∠F=30°,
∴HF=DF•cos30°=
DF,
∴CF=CH+FH=AE+
DF.
(3) 结论:CF=
DF-AE.
理由:如图3中,作DH⊥FC于H.
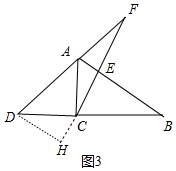
同法可证△DCH≌△CAE,
∴AE=CH,
在Rt△DHF中,∵∠DHF=90°,∠F=30°,
∴HF=DF•cos30°=
DF,
∴CF=FH-CH=
DF-AE.

在Rt△ACB中,AB=10,AC=x,BC=CD+BD=x+2,
∵AB2=AC2+BC2,
∴102=x2+(x+2)2,
解得x=6或-8(舍弃),
∴AC=6.
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| 6×8 |
| 10 |
| 24 |
| 5 |
(2)证明:如图2中,作DH⊥CF于H.

∵∠ACD=∠AEC=∠DHC=90°,
∴∠ACE+∠CAE=90°,∵∠ACE+∠BCE=90°,
∴∠CAE=∠DCH,
在△ACE和∠CDH中,
|
∴△ACE≌△CDH,
∴AE=CH,
在Rt△DHF中,∵∠DHF=90°,∠F=30°,
∴HF=DF•cos30°=
| ||
| 2 |
∴CF=CH+FH=AE+
| ||
| 2 |
(3) 结论:CF=
| ||
| 2 |
理由:如图3中,作DH⊥FC于H.

同法可证△DCH≌△CAE,
∴AE=CH,
在Rt△DHF中,∵∠DHF=90°,∠F=30°,
∴HF=DF•cos30°=
| ||
| 2 |
∴CF=FH-CH=
| ||
| 2 |
看了 如图1,在Rt△ABC中,∠...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
O、A、B、C为空间四个点,又OA、OB、OC为空间的一个基底,则()A.O、A、B、C四点不共线 2020-05-14 …
A与B有如下的反应:A+B生成C+D 若c为厨房内常用的调味品,在A溶液中加入铁粉能产生氢气,则A 2020-05-16 …
关于正弦定理解题a、b、c为三角形三边,若c^2=a^2+b^2,则三角形为直角三角形问:1、a、 2020-05-22 …
关于化学反应A+B=C+D,下列说法中正确的是:A.若C是单质,D为化合物,则A和B中一定有一种是 2020-06-06 …
据图分析下列叙述正确的是()A.若图中a为下丘脑、b为垂体、c为甲状腺,则物质e的增加会直接导致d 2020-06-19 …
阅读理若A、B、C为数轴上三点且点C在点A、点B之间,若点C到A的距离是点C到B的距离2倍,我们就 2020-07-14 …
求绿地面积A,B,C为坐落在一条南北走向的公路沿线上的三个汽车站,其中AB、BC的距离分别为3千米和 2020-11-21 …
如图为人体某结构内的血管结构和血液流动方向示意图:(1)若c为肺泡外的毛细血管,则a内流动的是血,b 2020-12-24 …
A、B、C为初中化学常见物质,它们之间的转化关系为:A→B→C.(1)若A、B、C均为氧化物,且A、 2021-02-03 …