早教吧作业答案频道 -->数学-->
如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.(1)依题意,补全图形;(2)求证:四边形EFMN是矩形;(3)连接DM,若DM⊥AC于点M,ON
题目详情
如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
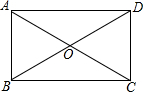
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.

(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
▼优质解答
答案和解析
(1) 如图所示:
(2)证明:∵点E,F分别为OA,OB的中点,
∴EF∥AB,EF=
AB,
同理:NM∥CD,MN=
DC,
∵四边形ABCD是矩形,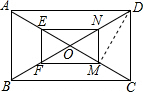
∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,
∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,
∴EO=
AO,MO=
CO,
在矩形ABCD中,AO=CO=
AC,BO=DO=
BD,
∴EM=EO+MO=
AC,
同理可证FN=
BD,
∴EM=FN,
∴四边形EFMN是矩形.
(3) ∵DM⊥AC于点M,
由(2)MO=
CO,
∴DO=CD,
在矩形ABCD中,
AO=CO=
AC,BO=DO=
BD,AC=BD,
∴AO=BO=CO=DO,
∴△COD是等边三角形,
∴∠ODC=60°,
∵MN∥DC,
∴∠FNM=∠ODC=60°,
在矩形EFMN中,∠FMN=90°.
∴∠NFM=90°-∠FNM=30°,
∵NO=3,
∴FN=2NO=6,FM=3
,MN=3,
∵点F,M分别为OB,OC的中点,
∴BC=2FM=6
,
∴矩形的面积为BC•CD=36
.
(2)证明:∵点E,F分别为OA,OB的中点,
∴EF∥AB,EF=
| 1 |
| 2 |
同理:NM∥CD,MN=
| 1 |
| 2 |
∵四边形ABCD是矩形,

∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,
∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,
∴EO=
| 1 |
| 2 |
| 1 |
| 2 |
在矩形ABCD中,AO=CO=
| 1 |
| 2 |
| 1 |
| 2 |
∴EM=EO+MO=
| 1 |
| 2 |
同理可证FN=
| 1 |
| 2 |
∴EM=FN,
∴四边形EFMN是矩形.
(3) ∵DM⊥AC于点M,
由(2)MO=
| 1 |
| 2 |
∴DO=CD,
在矩形ABCD中,
AO=CO=
| 1 |
| 2 |
| 1 |
| 2 |
∴AO=BO=CO=DO,
∴△COD是等边三角形,
∴∠ODC=60°,
∵MN∥DC,
∴∠FNM=∠ODC=60°,
在矩形EFMN中,∠FMN=90°.
∴∠NFM=90°-∠FNM=30°,
∵NO=3,
∴FN=2NO=6,FM=3
| 3 |
∵点F,M分别为OB,OC的中点,
∴BC=2FM=6
| 3 |
∴矩形的面积为BC•CD=36
| 3 |
看了 如图,矩形ABCD的对角线A...的网友还看了以下:
如图,抛物线y=ax的平方+bx+c的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.( 2020-05-16 …
如图,数轴上点A,C对应的数分布是a,c,且a,c满足|a+4|+(c-1)2=0,点B对应的数是 2020-07-22 …
已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),已知关于x的二次函数y 2020-07-23 …
如图,数轴上点A、C对应的数分别为a、c,且a、c满足|a+4|+(c-1)2=0.,点B对应的数 2020-07-30 …
几道函数题1已知点A(4,3),点B(0,1),若点C是x轴上一动点,当AC+BC的值最小时,求C 2020-07-30 …
A(1,3).B(-3,1).C(-1,-4).D(5,-2).P(3,4)为平面直角坐标系内五个 2020-07-31 …
(1)已知a+b=-c,则a(1/a+1/b)+b(1/a+1/c)+c(1/a+1/b)的值是多少 2020-10-31 …
已知A、B两点在数轴上的位置如图所示,C是数轴上的另外一点,设点A、B、C对应的有理数分别为a、b、 2020-11-01 …
设函数f(x)=(1/2)x^2+4lnx+c(1)当c=1时,求函数f(x)在[1,2e]上的最大 2020-12-08 …
如图为一突触的结构,在a、d两点连接一个灵敏电流计.已知ab=bd,若分别刺激b、c两点,灵敏电流计 2020-12-30 …