早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.(1)若BD2+CE2=DE2,则∠BAC的度数;(2)若∠ABC的平分线BF和边AC的垂直平分线EF相交于点F,过点F作FG垂直于BA的延长线
题目详情
如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.
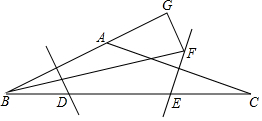
(1)若BD2+CE2=DE2,则∠BAC的度数;
(2)若∠ABC的平分线BF和边AC的垂直平分线EF相交于点F,过点F作FG垂直于BA的延长线于点G.求证:BC-AB=2AG.

(1)若BD2+CE2=DE2,则∠BAC的度数;
(2)若∠ABC的平分线BF和边AC的垂直平分线EF相交于点F,过点F作FG垂直于BA的延长线于点G.求证:BC-AB=2AG.
▼优质解答
答案和解析
(1)如图1中,连接AD、AE.
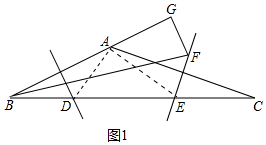
∵边AB、AC的垂直平分线分别交BC于点D、E,
∴BD=DA,EA=EC,
∴∠DBA=∠DAB,∠EAC=∠C,设∠DBA=∠DAB=x,∠EAC=∠C=y,
∵BD2+CE2=DE2,
∴AD2+AE2=DE2,
∴∠DAE=90°,
∴2x+90°+2y=180°,
∴x+y=45°,
∴∠BAC=x+y+90°=135°.
(2)证明:如图2中,连接AF,FC,作FM⊥CB于M,
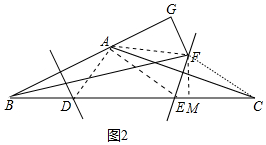
∵BF平分∠CBA,FG⊥BA,FM⊥CB,
∴FG=FM(角平分线上的点到角的两边距离相等),
在Rt△BFG和Rt△BFM中,
∴Rt△BFG≌Rt△CFM,
∴BG=BM,
∵EF垂直平分线AC,
∴FA=FC(垂直平分线上的点到线段两端点距离相等),
∵FG=FM,∠AFD=∠DMB=90°,
在Rt△AFG和Rt△CFM中,
,
∴Rt△AFG≌Rt△CFM,
∴CM=AG,
∵BC=BM+CM,BG=AB+AG,BG=BM,CM=AG,
∴BC=AB+2AG,
∴BC-AB=2AG.

∵边AB、AC的垂直平分线分别交BC于点D、E,
∴BD=DA,EA=EC,
∴∠DBA=∠DAB,∠EAC=∠C,设∠DBA=∠DAB=x,∠EAC=∠C=y,
∵BD2+CE2=DE2,
∴AD2+AE2=DE2,
∴∠DAE=90°,
∴2x+90°+2y=180°,
∴x+y=45°,
∴∠BAC=x+y+90°=135°.
(2)证明:如图2中,连接AF,FC,作FM⊥CB于M,

∵BF平分∠CBA,FG⊥BA,FM⊥CB,
∴FG=FM(角平分线上的点到角的两边距离相等),
在Rt△BFG和Rt△BFM中,
|
∴Rt△BFG≌Rt△CFM,
∴BG=BM,
∵EF垂直平分线AC,
∴FA=FC(垂直平分线上的点到线段两端点距离相等),
∵FG=FM,∠AFD=∠DMB=90°,
在Rt△AFG和Rt△CFM中,
|
∴Rt△AFG≌Rt△CFM,
∴CM=AG,
∵BC=BM+CM,BG=AB+AG,BG=BM,CM=AG,
∴BC=AB+2AG,
∴BC-AB=2AG.
看了 如图,在△ABC中,∠BAC...的网友还看了以下:
1若以2、3、x为三遍组成一个锐角三角形,则x的范围是?2在三角形abc中,内角A.B.C的对边分别 2020-03-31 …
在三角形ABC中 角A B C所对的边分别为a b c,若a=根号2 b=2 sinB+cosB= 2020-04-05 …
在三角形abc中,A、B、C的对边分别为a、b、c若(a2+c2-b2)tan=根3ac,则角B的 2020-05-21 …
“他们为后人在岔路口插了若干‘此路不通’的木牌”这句话的意思是()A.失败者生命的轨迹,为成功者提 2020-06-18 …
在△ABC中,角A,B,C所对的边分别为a,b,c,若b-½c=acosC②若三角形的面积为2在△ 2020-07-23 …
1.在三角形ABC中,LA=二分之一LB=三分之一LC,它的最长边为10cm,则此三角形得最短边为 2020-07-27 …
若a,b,c是直角三角形的三条边长,斜边上c上的高长是h,给出下列的结论:若a,b,c是Rt△的3 2020-07-30 …
(1)在RT三角形ABC中,角C=90°,a.b.c分别为其三边,c为斜边,若c+a=18,c-a 2020-08-04 …
(2012•长沙模拟)在△ABC中,角A,B,C的对边分别为a,b,c,若sinA=sinB=sin 2020-10-30 …
如图已知双曲线y=k/x(k>0)经过直角三角形OAB斜边OB的中点D且与直角边AB相交于点C若DE 2020-11-27 …