早教吧作业答案频道 -->数学-->
如图,直线AB与CD相交于点O.(1)若∠AOD+∠COB=2(∠BOD+∠AOC),求∠AOD,∠BOD的度数.(2)若∠COB-∠BOD=m°,求∠AOD,∠BOD的度数(用含m°的式子表示)
题目详情
如图,直线AB与CD相交于点O.
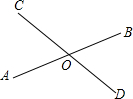
(1)若∠AOD+∠COB=2(∠BOD+∠AOC),求∠AOD,∠BOD的度数.
(2)若∠COB-∠BOD=m°,求∠AOD,∠BOD的度数(用含m°的式子表示)

(1)若∠AOD+∠COB=2(∠BOD+∠AOC),求∠AOD,∠BOD的度数.
(2)若∠COB-∠BOD=m°,求∠AOD,∠BOD的度数(用含m°的式子表示)
▼优质解答
答案和解析
∵直线AB与CD相交与点O,
∴∠AOD=∠COB,∠BOD=∠AOC.
∵∠AOD+∠COB=2(∠BOD+∠AOC),
∴∠AOD=2∠BOD.
∵∠AOD+∠BOD=180°,
∴3∠AOD=180°.
∴∠AOD=60°.
∴∠AOD=180°-∠BOD=120°.
(2)∵∠COB+∠BOD=180°,
∴∠COB=180°-∠BOD.
∵∠COB-∠BOD=m°,
∴180°-2∠BOD=m°.
∴∠BOD=90°-
m°,
∵∠AOD+∠BOD=180°,
∴∠AOD=180°-∠BOD=180°-(90°-
m°)=90°+
m°.
∴∠AOD=∠COB,∠BOD=∠AOC.
∵∠AOD+∠COB=2(∠BOD+∠AOC),
∴∠AOD=2∠BOD.
∵∠AOD+∠BOD=180°,
∴3∠AOD=180°.
∴∠AOD=60°.
∴∠AOD=180°-∠BOD=120°.
(2)∵∠COB+∠BOD=180°,
∴∠COB=180°-∠BOD.
∵∠COB-∠BOD=m°,
∴180°-2∠BOD=m°.
∴∠BOD=90°-
| 1 |
| 2 |
∵∠AOD+∠BOD=180°,
∴∠AOD=180°-∠BOD=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
看了 如图,直线AB与CD相交于点...的网友还看了以下:
如图所示,将△OBA进行怎样的平移可得到△O′B′A′?并分别写出△OBA和△O′B′A′各顶点的 2020-05-13 …
O、A、B、C为空间四个点,又OA、OB、OC为空间的一个基底,则()A.O、A、B、C四点不共线 2020-05-14 …
如图,等边三角形ABO放在平面直角坐标系中,其中点O为坐标原点,点B的坐标为(-8,0),点A位于 2020-06-08 …
直线y=-34x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止. 2020-06-12 …
现有固定的光滑直杆AB和光滑弧管道BC,两者在B处相切并平滑连接,O为圆心.O、A在同一条水平线上 2020-07-17 …
已知O、A、M、B为平面上四点,且OM=λOB+(1-λ)OA,λ∈(1,2),则()A.点M在线 2020-07-24 …
读图3和图4,回答18~19题。小题1:据各自然带在图3中的位置,能得出的正确结论是()A.O→a距 2020-11-10 …
作一个角等于∠AOB,在射线O′A′上,以O′为圆心,以OC长为半径画弧,交O′A′于点C′,再以( 2020-12-09 …
甲、乙、丙、丁等四个人的血型各不相同,若用A型血清检查,发现丙、丁的血液有凝集反应,而且经检验,丙只 2020-12-24 …
直线y=-34x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点匀速出发,同时到达A点,到达A时 2020-12-27 …