早教吧作业答案频道 -->数学-->
已知△ABC的面积是60,请完成下列问题:(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积△ACD的面积(填“>”“<”或“=”)(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线
题目详情
已知△ABC的面积是60,请完成下列问题:
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积___△ACD的面积(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=
S△ABC=30,S△ADC=
S△ABC=30,可列方程组为:
,解得___,通过解这个方程组可得四边形ADOE的面积为___.
(3)如图3,AD:DB=1:3,CE:AE=1:2,请你计算四边形ADOE的面积,并说明理由.
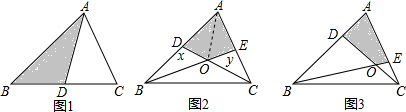
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积___△ACD的面积(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| |
|
(3)如图3,AD:DB=1:3,CE:AE=1:2,请你计算四边形ADOE的面积,并说明理由.

▼优质解答
答案和解析
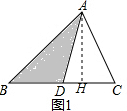 (1)如图1,过A作AH⊥BC于H,
(1)如图1,过A作AH⊥BC于H,
∵AD是△ABC的BC边上的中线,
∴BD=CD,
∴S△ABD=
BD•AH,S△ACD=
CD•AH,
∴S△ABD=S△ACD,
故答案为:=;
(2)解方程组得
,
∴S△AOD=S△BOD=10,
∴S四边形ADOB=S△AOD+S△AOE=10+10=20,
故答案为:得
,20;
(3)如图3,连结AO,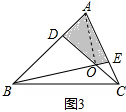
∵AD:DB=1:3,
∴S△ADO=
S△BDO,
∵CE:AE=1:2,
∴S△CEO=
S△AEO,
设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,
由题意得:S△ABE=
S△ABC=40,S△ADC=
S△ABC=15,
可列方程组为:
,
解得:
,
∴S四边形ADOE=S△ADO+S△AEO=x+2 y=13.
 (1)如图1,过A作AH⊥BC于H,
(1)如图1,过A作AH⊥BC于H,∵AD是△ABC的BC边上的中线,
∴BD=CD,
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABD=S△ACD,
故答案为:=;
(2)解方程组得
|
∴S△AOD=S△BOD=10,
∴S四边形ADOB=S△AOD+S△AOE=10+10=20,
故答案为:得
|
(3)如图3,连结AO,

∵AD:DB=1:3,
∴S△ADO=
| 1 |
| 3 |
∵CE:AE=1:2,
∴S△CEO=
| 1 |
| 2 |
设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,
由题意得:S△ABE=
| 2 |
| 3 |
| 1 |
| 4 |
可列方程组为:
|
解得:
|
∴S四边形ADOE=S△ADO+S△AEO=x+2 y=13.
看了 已知△ABC的面积是60,请...的网友还看了以下:
在锐角三角形中,abc分别为角ABC的对边,c=根号21b=4且BC边上的高h=2倍根号3(1)求角 2020-03-30 …
在三角形ABC中,角A,B,C所对的边分别为a,b,c,若a+b=c(cosA+cosB)(1)判 2020-04-07 …
直角三角形中,两条直角边a,b和斜边c之间满足下面的关系:a2+b2=c2.如果一个直角三角形的斜 2020-05-13 …
已知a、b、c是一直角三角形的三边,c是斜边,且均为正整数,a为质数;求证明已知a、b、c是一直角 2020-05-17 …
有兴趣进来有三个相同的砝码a、b、c,用三根相同的绳子相连,a用绳子A固定在顶上,b用绳子B连接在 2020-07-12 …
定义:在△ABC中,∠C=30°,我们把∠A的对边与∠C的对边的比叫做∠A的邻弦,记作thiA,即 2020-07-22 …
两圆重合面积问题A圆/B圆的直径分别为:a,b两圆的圆心距离为c(c=a.补充:B圆在A圆的右边, 2020-07-24 …
如图,已知Rt三角形ABC的面积是11,角C=90,两条直角边a,b的和为12,求这个直角三角形的 2020-07-30 …
利用余弦定理求出下题:已知△ABC的∠A为43°,且a=7km、c=3km(a是∠A的对边,b是∠ 2020-08-02 …
哥哥姐姐来帮帮1,若直角三角形的两个锐角只差为24度,则较大的锐角是几度?2直角三角形ABC中的斜边 2020-11-08 …