如图，AB是⊙O的直径，BC为弦，D为AC的中点，AC，BD相交于E点，过点A作⊙O的切线交BD的延长线于P点．（1）求证：∠PAC=2∠CBE；（2）若PD=m，∠CBE=α，请写出求线段CE长的思路．

Question

如图，AB是⊙O的直径，BC为弦，D为

AC

的中点，AC，BD相交于E点，过点A作⊙O的切线交BD的延长线于P点．

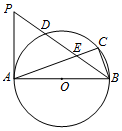
（1）求证：∠PAC=2∠CBE；
（2）若PD=m，∠CBE=α，请写出求线段CE长的思路．

Answer 1

（1）证明：∵D为

AC

的中点
∴∠CBA=2∠CBE，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠1+∠CBA=90°，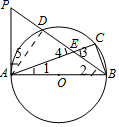
∴∠1+2∠CBE=90°，
∵AP是⊙O的切线，
∴∠PAB=∠1+∠PAC=90°，
∴∠PAC=2∠CBE，

（2）思路：①连接AD，由D是

AC

的中点，∠2=∠CBE，
由∠ACB=∠PAB=90°，得∠P=∠3=∠4，故AP=AE；
②由AB是⊙O的直径，可得∠ADB=90°；由AP=AE，
得PE=2PD=2m，∠5=(1)/(2)∠PAC=∠CBE=α，
③在Rt△PAD中，由PD=m，∠5=α，可求PA的长
④在Rt△PAB中，由PA的长和∠2=α，可求BP的长；
由BE=PB-PE可求BE的长；
⑤在Rt△BCE中，由BE的长和∠CBE=α，可求CE的长．