早教吧作业答案频道 -->数学-->
如图,AB是O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.(1)求证:BF是O的切线;(2)已知圆的半径为1,求EF的长.
题目详情
如图,AB是 O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作 O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
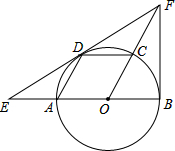
(1)求证:BF是 O的切线;
(2)已知圆的半径为1,求EF的长.

(1)求证:BF是 O的切线;
(2)已知圆的半径为1,求EF的长.
▼优质解答
答案和解析
(1)证明:连结OD,如图,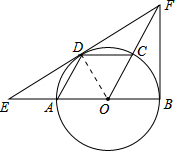 ∵四边形AOCD是平行四边形,
∵四边形AOCD是平行四边形,
而OA=OC,
∴四边形AOCD是菱形,
∴△OAD和△OCD都是等边三角形,
∴∠AOD=∠COD=60°,
∴∠FOB=60°,
∵EF为切线,
∴OD⊥EF,
∴∠FDO=90°,
在△FDO和△FBO中
,
∴△FDO≌△FBO,
∴∠ODF=∠OBF=90°,
∴OB⊥BF,
∴BF是 O的切线;
(2) 在Rt△OBF中,∵∠FOB=60°,
而tan∠FOB=
,
∴BF=1×tan60°=
.
∵∠E=30°,
∴EF=2BF=2
.
 ∵四边形AOCD是平行四边形,
∵四边形AOCD是平行四边形,而OA=OC,
∴四边形AOCD是菱形,
∴△OAD和△OCD都是等边三角形,
∴∠AOD=∠COD=60°,
∴∠FOB=60°,
∵EF为切线,
∴OD⊥EF,
∴∠FDO=90°,
在△FDO和△FBO中
|
∴△FDO≌△FBO,
∴∠ODF=∠OBF=90°,
∴OB⊥BF,
∴BF是 O的切线;
(2) 在Rt△OBF中,∵∠FOB=60°,
而tan∠FOB=
| BF |
| OB |
∴BF=1×tan60°=
| 3 |
∵∠E=30°,
∴EF=2BF=2
| 3 |
看了 如图,AB是O的直径,点C、...的网友还看了以下:
AB为圆O的直径,点C为圆O上的一点,AD和过点C的切线互相垂直,垂足为点D过点D作CE垂直于AB 2020-05-21 …
求助一道平面几何题延长圆O的直径AB到C,使OB=BC,直线CD切圆O于D,AE垂直于CD,垂足为 2020-06-06 …
AB是圆O的直径AB=6角CAD=30度,求弦长DCOA是圆O的半径,以OA为直径的圆C与圆O的弦 2020-06-06 …
(2013•朝阳区一模)如图,⊙O是△ABC是的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在 2020-06-15 …
(2002•海淀区)如图,AB是⊙O的直径,AE平分∠BAF交⊙O于点E,过点E作直线与AF垂直交 2020-07-20 …
如图,AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,BC=3,CD=2AB是⊙O的直径 2020-07-21 …
延长⊙O的直径AB到P,使PB=OB,过P作PC切⊙O于C,过B作BD切⊙O于B,交PC于D.(1 2020-07-24 …
如图,已知AB是圆O的直径,点C、D在圆O上,点E在圆O外,角EAC=角D=60°(1)求证:A如 2020-07-31 …
如图,AB是⊙O的直径,过圆上一点D作⊙O的切线DE,与过点A的直线垂直于E,弦BD的延长线与直线 2020-07-31 …
求2009年的济南的中考数学题:已知AB是圆O的直径,CA与圆O相切于点A,连接CO交圆O于点D,C 2021-01-22 …