早教吧作业答案频道 -->数学-->
如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.(1)求AE的长;(2)点P从点B出发,以每秒1个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.①当t为何值时,CP
题目详情
如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.
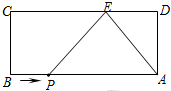
(1)求AE的长;
(2)点P从点B出发,以每秒1个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
①当t为何值时,CP=AE;
②当t为何值时,△PAE是以AE为腰的等腰三角形.

(1)求AE的长;
(2)点P从点B出发,以每秒1个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
①当t为何值时,CP=AE;
②当t为何值时,△PAE是以AE为腰的等腰三角形.
▼优质解答
答案和解析
(1)∵四边形ABCD是长方形,
∴CD=AB=9,BC=AD=4,∠D=90°,
∵CE=6,
∴DE=CD-CE=3,
∴AE=
=5;
(2)①根据题意得:BP=t,
∴CP=
=
,
∵CP=AE,
∴
=5,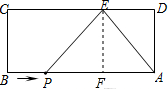
解得:t=3;
②若AP=AE=5,
∴BP=AB-AP=9-5=4,
∴t=4;
若PE=AE=5,则过点E作EF⊥AB于点F,
则四边形ADEF是矩形,
∴PF=AF=DE=3,
∴AP=AF+PF=6,
∴t=BP=AB-AP=3.
综上所述,当t=3或t=4时,△PAE是以AE为腰的等腰三角形.
∴CD=AB=9,BC=AD=4,∠D=90°,
∵CE=6,
∴DE=CD-CE=3,
∴AE=
| AD2+DE2 |
(2)①根据题意得:BP=t,
∴CP=
| BC2+CP2 |
| 16+t2 |
∵CP=AE,
∴
| 16+t2 |

解得:t=3;
②若AP=AE=5,
∴BP=AB-AP=9-5=4,
∴t=4;
若PE=AE=5,则过点E作EF⊥AB于点F,
则四边形ADEF是矩形,
∴PF=AF=DE=3,
∴AP=AF+PF=6,
∴t=BP=AB-AP=3.
综上所述,当t=3或t=4时,△PAE是以AE为腰的等腰三角形.
看了 如图,长方形ABCD中,AB...的网友还看了以下:
已知椭圆C:若半焦距c=2√2,且2/3,e,4/3成等比数列.求椭圆C的方程 2020-05-15 …
如图,多边形ABCDEF的顶点坐标为A(-2,2)B(-2,-2),C(4,-2),D(4,0)E 2020-05-16 …
怎样使用matlab解下面的代数方程?急.syms a b c d e;2*b^2=a^2+c^2 2020-05-16 …
求极限lim[cosx-e^(-x^2/2)]/x^4 其中x趋向于0.我的做法为什么错了:lim 2020-05-16 …
如果做左腕。X线摄片,可显示的骨化中心数最多为A.0个B.1个C.3个D.2个E.4个 2020-06-04 …
已知a[1,0].b0,-1]c[-1,2].d[2,-1]e[4,2]五个点,抛物线y=a[x- 2020-07-09 …
3、下列常数中哪些是符合C语法规定的:(A)‘\’(B)e3(C)“ab\n”(D)(2+3)e(4 2020-10-31 …
maple不等方程组solve({-(-u^3/3-e*u^2/2+u)>-(e^2+4)^(3/2 2020-10-31 …
多选一下贷款期限属于中期贷款的()A.3个月B.1年C.1.5年D.2年E.4年多选一下贷款期限属于 2020-11-06 …
已知正数,a,b,c,d,c,e,f,都是正数,且bcdef/a=1/2,acdef/b=1/4,a 2020-12-23 …