早教吧作业答案频道 -->数学-->
如图,O是△ABC内一点,O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC,连接DF、EG.(1)求证:AB=AC.(2)已知AB=10,BC=12,求四边形DFGE是矩形时O的半径.
题目详情
如图,O是△ABC内一点, O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC,连接DF、EG.
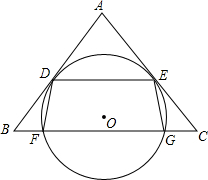
(1)求证:AB=AC.
(2)已知AB=10,BC=12,求四边形DFGE是矩形时 O的半径.

(1)求证:AB=AC.
(2)已知AB=10,BC=12,求四边形DFGE是矩形时 O的半径.
▼优质解答
答案和解析
(1)证明:∵AD、AE是 O的切线,
∴AD=AE,
∴∠ADE=∠AED,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠B=∠C,
∴AB=AC;
(2) 如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设 O半径为r,
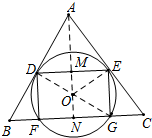
∵四边形DFGE是矩形,
∴∠DFG=90°,
∴DG是 O直径,
∵ O与AB、AC分别相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵OD=OE,OE⊥AC,
∵OD=OE.
∴AN平分∠BAC,∵AB=AC,
∴AN⊥BC,BN=
BC=6,
在RT△ABN中,AN=
=
=8,
∵OD⊥AB,AN⊥BC,
∴∠ADO=∠ANB=90°,
∵∠OAD=∠BAN,
∴△AOD∽△ABN,
∴
=
,即
=
,
∴AD=
r,
∴BD=AB-AD=10-
r,
∵OD⊥AB,
∴∠GDB=∠ANB=90°,
∵∠B=∠B,
∴△GBD∽△ABN,
∴
=
,即
=
,
∴r=
,
∴四边形DFGE是矩形时 O的半径为
.
∴AD=AE,
∴∠ADE=∠AED,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠B=∠C,
∴AB=AC;
(2) 如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设 O半径为r,

∵四边形DFGE是矩形,
∴∠DFG=90°,
∴DG是 O直径,
∵ O与AB、AC分别相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵OD=OE,OE⊥AC,
∵OD=OE.
∴AN平分∠BAC,∵AB=AC,
∴AN⊥BC,BN=
| 1 |
| 2 |
在RT△ABN中,AN=
| AB2-BN2 |
| 102-62 |
∵OD⊥AB,AN⊥BC,
∴∠ADO=∠ANB=90°,
∵∠OAD=∠BAN,
∴△AOD∽△ABN,
∴
| OD |
| BN |
| AD |
| AN |
| r |
| 6 |
| AD |
| 8 |
∴AD=
| 4 |
| 3 |
∴BD=AB-AD=10-
| 4 |
| 3 |
∵OD⊥AB,
∴∠GDB=∠ANB=90°,
∵∠B=∠B,
∴△GBD∽△ABN,
∴
| BD |
| BN |
| GD |
| AN |
10-
| ||
| 6 |
| 2r |
| 8 |
∴r=
| 60 |
| 17 |
∴四边形DFGE是矩形时 O的半径为
| 60 |
| 17 |
看了 如图,O是△ABC内一点,O...的网友还看了以下:
跳台滑雪运动员经过一段加速滑行后从0点水平飞出,经过3s后到斜坡上的A点,已知C点 .运动员落到A 2020-05-17 …
两同学用如图所示方法做共点力平衡实验.M、N为摩擦不计的定滑轮,O点是轻质细绳OA、OB和OC的结 2020-06-14 …
如图所示,物块m由高h的A处静止释放后沿斜面运动到B,再沿水平面运动后停在C处,已知物块与斜面及水 2020-06-16 …
某汽车在平直公路上从A点出发,向东行驶x1=100m后到达B点,又向东偏北θ=60°的方向沿直线驶 2020-07-11 …
如图,已知P为正方形ABCD内一点,以点B为旋转中心,将△ABP顺时针旋转使A点和C点重合,这时P 2020-07-11 …
如图所示,静止在粗糙水平面上的斜面体有三个光滑斜面AB、AC和CD.已知斜面AB与水平方向成37° 2020-07-17 …
如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到C点在圆锥的侧面上的最短距 2020-07-20 …
如图,在数轴上A点表示数a,B点表示数b,C点表示数c.且a、c满足|a+3|+(c-7)2=0. 2020-07-30 …
已知,如图,直径为OA的圆心M与X轴交于点O,A,点B,C把弧OA分为三等份,连接MC并延长交于Y轴 2020-11-27 …
如图所示,有一皮带传动装置,A、B、C三点到各自转轴的距离分别为RA、RB、RC,已知RB=RC=R 2020-12-12 …