早教吧作业答案频道 -->物理-->
如图所示,一水池深为h,一根长直木棍竖直地插入水底,棍露出水面部分的长度L,当太阳光与水平面夹角为60°斜射到水面时,求棍在水底的影子的长度.(已知水的折射率为n)
题目详情
如图所示,一水池深为h,一根长直木棍竖直地插入水底,棍露出水面部分的长度L,当太阳光与水平面夹角为60°斜射到水面时,求棍在水底的影子的长度.(已知水的折射率为n)

▼优质解答
答案和解析
如图所示为光路图,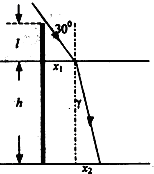
水面部分的投影长为x1=Ltan30°,
设光从空气进入水中的折射角为γ,根据折射定律得,
=n,
则可得cosγ=
,tanγ=
,
根据几何关系可得x2=htanγ=
.
即棍在水底的影子长度为x=x1+x2=
+
.
答:棍在水底的影子的长度为
+
.

水面部分的投影长为x1=Ltan30°,
设光从空气进入水中的折射角为γ,根据折射定律得,
| sin30° |
| sinγ |
则可得cosγ=
| ||
| 2n |
| 1 | ||
|
根据几何关系可得x2=htanγ=
| h | ||
|
即棍在水底的影子长度为x=x1+x2=
| ||
| 3 |
| h | ||
|
答:棍在水底的影子的长度为
| ||
| 3 |
| h | ||
|
看了 如图所示,一水池深为h,一根...的网友还看了以下:
将长为38cm,宽为5cm的长方形白纸,按如图所示方法粘合在一起,粘合部分白纸为2cm.(1)求1 2020-06-21 …
将长为38cm,宽为5cm的长方形白纸,按如图所示方法粘合在一起,粘合部分白纸为2cm.(1)求1 2020-06-21 …
一个建筑物上部为四棱锥,下部为长方体,长方体的上底面尺寸与四棱锥下底面一样,已知长方体长20m,宽 2020-07-16 …
要做一个底面为长方形的带盖的箱子,其体积为72cm3,其底面两邻边长之比为1∶2,则它的长为,宽为 2020-07-30 …
一个IP报头的头长度字段为4位,当其值为0101(2进制)时以下说法正确的是()A.此IP报数据部分 2020-11-07 …
一道初2数学题如图,某农科所有一块长方形试验基地,面积为2000m平方.现要将其分为A,B,C,D四 2020-11-18 …
一道数学简答题在一块长为45米、宽为30米的长方形空地上,修建两个底部是长方形且底部面积为192平方 2020-12-03 …
物体由倾角为θ,长为L的斜面顶端开始无初速下滑,若斜面是光滑的,则物体滑下的加速度大小为,末速度大小 2020-12-09 …
如图所示,为一传送货物的传送带abc,传送带的ab部分与水平面夹角=37°,bc部分与水平面夹角=5 2020-12-12 …
对于常温下一根阻值为R的金属电阻丝,下列说法正确的是()A.常温下,若将电阻丝均匀拉长为原来的10倍 2020-12-31 …